6

We can inscribe a cube in dodecahedron (see this), where $12$ faces of dodecahedron give the $12$ edges of the cube.

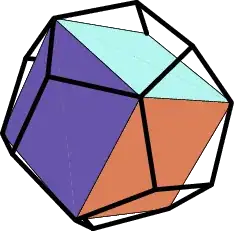
enter image description here

Can we inscribe cube in icosahedron?

Community
  • 1
Groups
  • 10,534
  • Which features would correspond? The $6$/$8$/$12$ faces/vertices/edges of a cube with the ... ? – Zubin Mukerjee Jan 11 '15 at 11:12
  • I didn't see any connection with the number of vertices/edges/faces between these two. But I thought there could be other way to inscribe a cube in icosahedron; since I don't know it, I posted it as a question. – Groups Jan 11 '15 at 12:08

1 Answers1

6

Dodecahedron and icosahedron are dual to one another. So there would be a way where each vertex of the icosahedron corresponds to an edge of the cube. So you'd have corners of the cube in the centers of some of the faces.

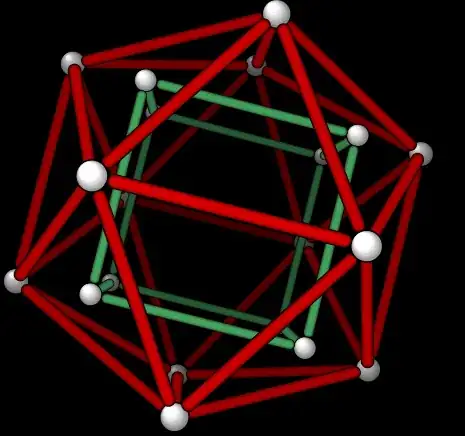
Cube in Icosahedron

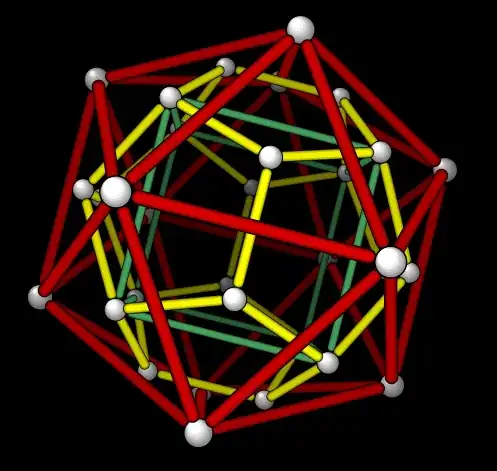
Cube in Dodecahedron in Icosahedron

Pictures created using a Cinderella Application created by J. Richter-Gebert.

MvG
  • 44,006