Another Monty Hall Question

Question

I still do not believe the "correct" solution to the Monty Hall Problem.

Here is my reasoning: The player can pick from $1$ of $3$ doors. The prize can be behind $1$ of $3$ doors. Monty will open $1$ of $3$ doors.

$3 \times 3 \times 3 = 27$ possible sequences of events.

In $15$ of those possible events, Monty either opens the door the player picked or the door with the prize. Since Monty will not do either of those, these $15$ events are removed from the possibilities.

Of the remaining $12$ possibilities, $6$ times the player wins if he stays with his original pick and $6$ times he wins if he switches. It looks to me like the player has the same chance of winning whether he stays or switches.

Could someone please explain the flaw in my reasoning.

The "27 possible sequences of events" does not make sense at all, as you are assuming that the three doors are distinct (i.e., the one the player chooses, where the prize is, and the one that Monty opens). — Clarinetist, Jan 03 '15 at 05:31
I recommend watching the numberphile video on the topic https://www.youtube.com/watch?v=4Lb-6rxZxx0 — JMoravitz, Jan 03 '15 at 05:34
There is nothing to believe here. One has first to agree which events are equally likely (the TV station might put the prize always behind the same door) and the rest follows by simple reasoning... — Fabian, Jan 03 '15 at 06:30
@JMoravitz actually the extended math version is more interesting — Caran-d'Ache, Jan 03 '15 at 06:39
Monty's actions are constrained as follows: (1) He knows what's behind each door. (2) He must open a door. (3) He must open a door hiding a goat. Once you factor in these rules, the puzzle becomes obvious. — user4894, Jan 03 '15 at 06:59
Stop right there. The only thing that is difficult about the Monty Hall problem is exactly specifying what the problem is. You are not saying one thing about what the problem is. — gnasher729, Jan 03 '15 at 23:22

hmakholm left over Monica · Accepted Answer · 2015-01-03T06:51:57.463

The basic flaw in the reasoning is that it assumes that each of the 12 possible outcomes are equally likely -- because without such an assumption "same number of outcomes" does not translate into "equal probability".

In many simple probability situations we can get a plausible "all outcomes are equally likely" assumption from symmetry arguments. But that won't hold here because the group of outcomes where the contestant chose the prize door are fundamentally different from the group of outcomes where the contestant chose a non-prize door; the host have different amount of options in the two cases.

As a simpler illustration that it doesn't always work to assume that all the possibilities are equally likely, consider this different game:

First the contestant flips a fair coin.
If the coin came out heads, the host rolls a fair die once; otherwise the host keeps rolling the die again and again until he rolls 6.

Here there are a priori 12 outcomes: {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}. But some of them are impossible; if we exclude them there are only 7 outcomes: {H1, H2, H3, H4, H5, H6, T6}. In 6 of the cases the coin flip was head; only one cases was the tails.

Can we then conclude the odds of flipping heads is 6 to 1?

Of course not. The coin is still fair, and what happens after it is flipped can't influence the probability of coming up tails. So this shows that comparing numbers of outcomes doesn't always give true probabilities, which ruins your Monty Hall analysis.

Suzu Hirose · Answer 2 · 2015-01-03T06:56:21.107

The reason that your numbers come out like that is because there are two possible doors for Monty to open if the contestant has already picked the right answer, but only one possible door for Monty to open if the contestant has picked wrongly. In the "two possible doors" case, switching to either of the doors loses, but this only happens in 1/3 of cases, so it is not meaningful to count in this way.

Here is an image. D indicates the door opened, the right side is the contestant's initial choice, and the top indicates which doors Monty can open:

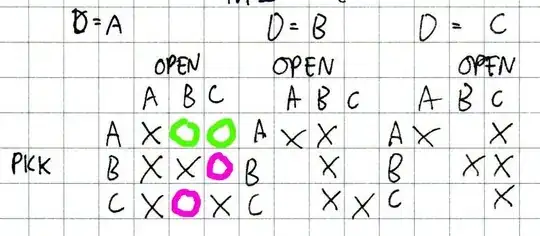
enter image description here

If the prize is at A (D=A above), the contestant picks A, then Monty can choose either B or C doors (as marked in green circles). If the contestant picks B when the correct answer is A, then Monty can open only C, and vice-versa if the contestant picks C (the pink circles are Monty's choices)

Assume that the contestant's pick $P$, the prize distribution $D$, and Monty's choice $M$ are uniformly distributed among the possibilities, then $$ P(M=B|P=A,D=A)=P(M=C|P=A,D=A)=1/2 $$ but $$ P(M=B|P=B,D=A)=0 $$ and $$ P(M=C|P=B,D=A)=1 $$ so since the pick and the prize are independent, $$ \begin{align} P(M=C,P=B,D=A)&=P(M=C|P=B,D=A) P(P=B) P(D=A)\\&=1\times\frac13\times\frac13\\&={1\over9} \end{align} $$ but $$ P(M=C,P=A,D=A)=P(M=C|P=A,D=A) P(P=A)P(D=A)={1\over18} $$ In other words the green circles only have probability $1/18$ whereas the pink circles have probability $1/9$.

The multiplicity of your counting just relates to Monty's freedom to choose either B or C when the contestant has the right answer.

score 4 · Answer 3 · answered Jan 03 '15 at 06:56

As another way to look at this, it might be helpful to think of a situation where it would be appropriate to use your calculation.

Suppose the game is played as follows: the player, the game studio, and Monty each secretly choose a door and write their choice on a piece of paper. A judge looks at the papers, and if Monty's choice is the same as the player's or the same as the studio's (i.e., where the prize is kept), then the papers are destroyed and the process is repeated—this will eliminate 15 of the 27 possibilities, as you have noted, and now the player has he same chance of winning whether he keeps his original choice or switches. Your calculation makes sense here.

This is different from the usual Monty Hall problem, however, because Monty normally makes his choice after the player and studio have already chosen.

Compare to the coin/die game in Henning Makholm's answer: if the coin and die were tossed simultaneously until you got a legal combination, then the odds of flipping heads would indeed be 6 to 1.

This argument is definitely wrong. – Suzu Hirose Jan 03 '15 at 07:02 — Suzu Hirose, Jan 03 '15 at 07:02
@SuzuHirose Would you care to elaborate? – Théophile Jan 03 '15 at 07:04 — Théophile, Jan 03 '15 at 07:04

j0equ1nn · Answer 4 · 2015-07-27T19:30:21.330

2

In my opinion the reason why the Monty Hall problem is confusing is because people make the solution unnecessarily complicated. I have a very simple solution that goes like this.

The player would win by switching doors if and only if (s)he chose the wrong door initially, which happens 2/3 of the time.

edited Jul 27 '15 at 19:30

answered Jul 26 '15 at 19:34

j0equ1nn

3,523

1

Yes, that's a solution in a nutshell. The question then is, when the OP tried a different solution method and came up with the wrong answer, exactly which steps of the "solution" were incorrect? – David K Jul 27 '15 at 20:31
@DavidK: I guess I don't see the point in sifting through long complicated incorrect solutions, when I have a very easy and correct one. Maybe this is from having to grade too many students' proofs :) In general I'd say it's a failure to consider the additional info from starting with 3 doors. – j0equ1nn Oct 22 '15 at 09:09
1

It can be useful to someone to learn from mistakes, but I doubt a student learns much from a mistake when all they find out is that a completely different approach to a particular problem gives a different answer. When I graded papers, I tried at least to identify the first incorrect step; but maybe this just shows I never graded enough papers to learn I shouldn't do that. :) – David K Oct 22 '15 at 13:25
1

In this case there's an obvious error in OP's argument: it assumes 27 events are equiprobable, using a model that is appropriate for three independent variables; but these variables are not independent in the problem statement, so the model is not justified. At least two answers have already expounded on this point, however, so I guess we can just leave it at that. – David K Oct 22 '15 at 13:29
@DavidK: Yeah, the other answers did cover what was wrong with the argument posed. I just like for people to know the solution need not be difficult or counterintuitive. I do think it's meaningful though to discuss what constitutes a valid proof, versus an intuitively sayisfying one (like Thurston's "Proof and Progress" article). – j0equ1nn Oct 22 '15 at 17:46
@DavidK I do the same thing when grading. Very time consuming. But often students reference unnecessarily complicated theory to get around a discomfort with basic stuff. I've seen people try to do Jacobians in response to a question about the distance between 2 points. In those cases they do learn from seeing the keep-it-simple approach. – j0equ1nn Oct 22 '15 at 17:53
1

OK, those are all good points. Both kinds of lessons are important. In fact there is a common thread, which is "use an appropriate approach." Avoid errors, but also don't overcomplicate things. – David K Oct 22 '15 at 18:35
This answer does not answer the question. – Dec 30 '21 at 05:05

score 1 · Answer 5 · answered Jan 03 '15 at 22:18

Monty does not have three choices, but only one or two. Initially before Monty opens a door the probabilities are as you expect:

You choose A, prize behind A: probability $\frac19$
You choose A, prize behind B: probability $\frac19$
You choose A, prize behind C: probability $\frac19$
You choose B, prize behind A: probability $\frac19$
You choose B, prize behind B: probability $\frac19$
You choose B, prize behind C: probability $\frac19$
You choose C, prize behind A: probability $\frac19$
You choose C, prize behind B: probability $\frac19$
You choose C, prize behind C: probability $\frac19$

Given this, Monty has to open a door which is not you initial choice and which is not the one with a prize. Sometimes Monty has a choice of door, and sometimes not, leading to $12$ possibilities with varying probabilities. Once Monty has opened a door, you can win or lose by switching and no further chance is involved as there are only two remaining doors. The probabilities become:

You choose A, prize behind A, Monty opens B: probability $\frac1{18}$, switching loses
You choose A, prize behind A, Monty opens C: probability $\frac1{18}$, switching loses
You choose A, prize behind B, Monty opens C: probability $\frac1{9}$, switching wins
You choose A, prize behind C, Monty opens B: probability $\frac1{9}$, switching wins
You choose B, prize behind A, Monty opens C: probability $\frac1{9}$, switching wins
You choose B, prize behind B, Monty opens A: probability $\frac1{18}$, switching loses
You choose B, prize behind B, Monty opens C: probability $\frac1{18}$, switching loses
You choose B, prize behind C, Monty opens A: probability $\frac1{9}$, switching wins
You choose C, prize behind A, Monty opens B: probability $\frac1{9}$, switching wins
You choose C, prize behind B, Monty opens A: probability $\frac1{9}$, switching wins
You choose C, prize behind C, Monty opens A: probability $\frac1{18}$, switching loses
You choose C, prize behind C, Monty opens B: probability $\frac1{18}$, switching loses

So overall switching wins with probability $6\times \dfrac19=\dfrac23$ and loses with probability $6\times \dfrac1{18}=\dfrac13$.

score 0 · Answer 6 · answered Jul 27 '15 at 20:41

If you want a set of outcomes with equal probability, you need to account somehow for the fact that when the contestant chooses the prize door on the first guess, Monty has a choice of which door to open.

This is best modeled as a random variable with two equally likely outcomes. We might as well assume Monty flips a coin and opens the leftmost possible door if the coin is heads, the rightmost possible door if the coin is tails. So:

Prize at A, contestant guesses A, coin is heads $\implies$ open door B.

Prize at A, contestant guesses A, coin is tails $\implies$ open door C.

Prize at A, contestant guesses B, coin is heads $\implies$ open door C.

Prize at A, contestant guesses B, coin is tails $\implies$ open door C.

These are four equally likely events. The difference with your "solution" is you only counted one A-B-C event and here there are two A-B-C events (A-B-heads-C and A-B-tails-C).

If you count all the possible outcomes including the coin flip every time (even when it isn't "needed") then you have 18 equally likely outcomes; 12 are winners and 6 are losers if you switch.

Another Monty Hall Question

6 Answers6

Linked