18

How many unit squares can overlap a given unit square without overlapping each other?

@calculus has managed to arrange 7 squares (see this GeogebraTube page). This seems like the maximum possible, but how to prove it formally?

Erel Segal-Halevi
  • 11,509
  • Have you tried putting the seventh square in the middle of the configuration, rather than round the outside? – Mark Bennet Dec 30 '14 at 15:23
  • You can put the seventh in the middle, since the diagonal is of greater length than the sides. There is space enough. The optimal configuration of overlapping is to be tangent. – Martigan Dec 30 '14 at 15:29
  • 5
    7 squares are possible: http://www.directupload.net/file/d/3852/a4wm5vz6_jpg.htm – callculus42 Dec 30 '14 at 15:55
  • @calculus Thanks! Now this seems absolutely full. But how can you prove that 8 are not possible? – Erel Segal-Halevi Dec 30 '14 at 19:30
  • 1
    @ErelSegalHalevi That is the difficulty of this problem. At the moment I have no idea how to prove it. But there is a great chance, that someone else have an idea. – callculus42 Dec 30 '14 at 20:09
  • I don't know if this helps but it sounds like the kissing number problem. Here is the similar question for non-overlapping squares from mathoverflow. Perhaps it inspire an idea as to the proof. http://mathoverflow.net/questions/117579/the-kissing-number-of-a-square-cube-hypercube – Bunny Aug 11 '15 at 21:22
  • Come to think of it couldn't you take the kissing number which proven to be 8 and then show that the overlapping number(which number what im calling the number in question) should be alteast or maybe even exactly one less, because that maybe the only decision that is possible in a situation- I dont know the technical term for that. – Bunny Aug 11 '15 at 21:36
  • @Red the connection with the Kissing number is interesting, thanks! I hope you or someone else can formalize it. – Erel Segal-Halevi Aug 12 '15 at 11:49
  • @Red the general relation between the kissing number and the overlapping number is interesting and I asked a separate question about it: http://mathoverflow.net/questions/214629/kissing-number-and-overlapping-number

    In any case, I don't think the difference is always one. For example, if we look at the family of axis-parallel unit-squares, the kissing-number is 8 but the overlapping-number is 4.

     – Erel Segal-Halevi Aug 12 '15 at 13:50

2 Answers2

11

Apparently $8$ squares are possible. Start with the example suggested by Peter Woolfitt and try to pack everything as tightly as possible.

In the following picture, each white square is tilted with respect to the gray square by a multiple of $\frac{\pi}{8}$ and the intersections are the obvious ones, i.e. each two squares intersect either in a whole side or in a single point.

enter image description here

Now perturb the angles and positions slightly so that the overlapping conditions are satisfied.

enter image description here

In case someone wants to play with this example, here is the Mathematica code used to produce the pictures. First, some useful functions:

ClearAll[A, T, sq]
A[phi_] := {{Cos[phi], -Sin[phi]}, {Sin[phi], Cos[phi]}}
T = {{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}};
sq[v_, phi_] := Line[Table[A[phi].t + v, {t, T}]]

The first picture:

Graphics[{Opacity[0.2], Polygon[T], Opacity[1], Gray, sq[{0, 0}, 0], 
  Black, sq[{0, 0}, 3 Pi/4], sq[{0, 0}, 5 Pi/4], sq[{0, 1}, 5 Pi/8], 
  sq[{0, 1}, Pi/8], sq[{1, 0}, -Pi/8], sq[{1, 0}, -5 Pi/8], 
  sq[{1, 1}, 0], sq[{1/2, (1 - Sqrt[2])/2} - {0.1, 0.1}, Pi/4]}]

The perturbation:

Graphics[{Opacity[0.2], Polygon[T], Opacity[1], Gray, sq[{0, 0}, 0], 
  Black, sq[{0, 0} + {0.01, 0.02}, 3 Pi/4], sq[{0, 0} + {0.02, 0.01}, 5 Pi/4], 
  sq[{0, 1} + {0.01, -0.01}, 5 Pi/8 - 0.05], sq[{0, 1} + {0.03, -0.01}, Pi/8 - 0.05], 
  sq[{1, 0} + {-0.01, 0.03}, -Pi/8 + 0.05], sq[{1, 0} + {-0.01, 0.01}, -5 Pi/8 + 0.05], 
  sq[{1, 1} - {0.01, 0.01}, 0], sq[{1/2, (1 - Sqrt[2])/2} - {0.12, 0.12}, Pi/4]}]
Dejan Govc
  • 17,347
9

This is a comment, but too large to fit in the comments section

Pure area arguments are unlikely to work as shown by this near miss for $8$ squares:

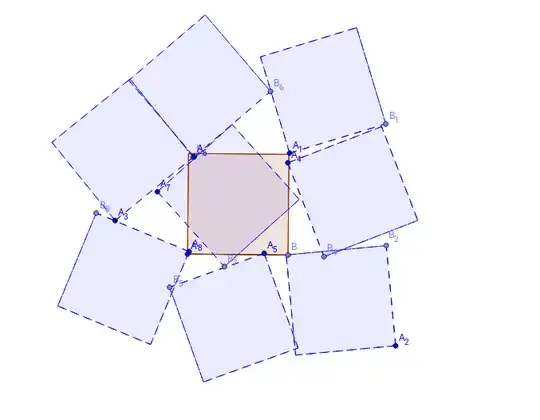
squares

Peter Woolfitt
  • 21,476