Let $P$ be a simple, planar polygon. Define $c_a$ as the area centroid of $P$, i.e., the center of gravity of the closed shape $P$. Define $c_p$ as the perimeter centroid of $P$, the center of gravity of just the boundary edges of $P$. One can compute $c_p$ as the weighted sum of the edge midpoints, weighted by their length, and normalized by the total perimeter of $P$.
My question is:
Q. Is there a clean characterization of those $P$ for which $c_a = c_p$?
Of course there are obvious examples (e.g., the regular polygons), but there are also non-obvious examples. Here is one I constructed:
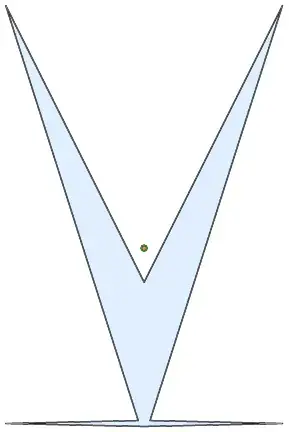
$$P= ((-1, 3), (-0.0426, 0), (-1, -0.0213), (0, -0.0426), (1, -0.0213), (0.0426, 0), (1, 3), (0, 1)) \;,\; \implies c_a =c_p = (0,1.247) $$
It seems these polygons are rare but not as uncommon as one might at first think. It would be interesting to quantify "rare" and "not as uncommon."