How prove this inequality $\sum\limits_{cyc}(a^2b+ab)\le 6$

Question

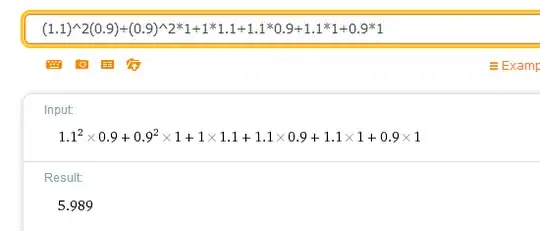
let $a,b,c> 0$ and such $a+b+c=3$

show that $$a^2b+b^2c+c^2a+ab+bc+ac\le 6?$$

I can't find counterexample, maybe it is true. Then how prove it?

And I know $$(a^2b+b^2c+c^2a)\le 4,a+b+c=3$$ see:Proving the inequality $4\ge a^2b+b^2c+c^2a+abc$ But this isn't useful

enter image description here

Doesn't matter. you can take $a \to 0$ that is very very small enough and $c=9/8-a$ — Sayan, Dec 27 '14 at 13:57
Hello,I think if $a,b,c$ are postive numbers,this inequality is true — math110, Dec 27 '14 at 14:30
When $a = \frac{11}{6}, b = \frac{9}{8}, c = \frac{1}{24}$, RHS = $\frac{83261}{13824} > 6$. Over the admissible range of $a,b,c$, RHS seems to be bounded from above by $\frac{26\sqrt{13}+70}{27} \approx 6.064604931928285$. — achille hui, Dec 27 '14 at 15:00
@chinamath apparently the inequality is true if $a \le b \le c$ and $b \le 1$ ! :-) — r9m, Dec 27 '14 at 15:38
because we only use $(b-a)(b-c)\le 0$,then we have$$a^2b+b^2c+c^2a\le b(a^2+ac+c^2)=b(a+c)^2-abc$$,so $$a^2b+b^2c+c^2a+ab+bc+ac\le b(a+c)^2+b(a+c)+(1-b)ac\le b(3-b)^2+b(3-b)+(1-b)\cdot(c+a)^2/4,0<b\le 1$$,then it is easy — math110, Dec 27 '14 at 15:44

score 2 · Answer 1 · answered Dec 27 '14 at 12:46

2

It's wrong! Try $c=0$ and $a+b=3$.

answered Dec 27 '14 at 12:46

Michael Rozenberg

2

The OP asks for $a,b,c>0$. Anyway, in your case, the inequality becomes $a^2b+ab=ab(a+1)\leq6$, or $a(a+1)(3-a)\leq6$, and it would be wrong in a small interval around $a=1.9$. With a tiny positive $c$ instead of $0$, your counterexample works, so +1 for me. For example, $a=1.9, b=1.09,c=0.01$ will do. – Jean-Claude Arbaut Dec 27 '14 at 14:48

1 Answers1