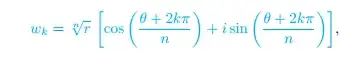0

$$f(z) = \frac{1}{z^4+4}$$

the roots of this are:

$z^2=\pm i\sqrt{2} \implies z=\pm\sqrt{i\sqrt{2}}$ and $z=\pm i\sqrt{i\sqrt{2}}$

i.e. $$f(z) = \frac{1}{(z\pm\sqrt{i\sqrt{2}})(\pm i\sqrt{i\sqrt{2}})}$$

i would like to know if there is a better simplification for this pole, since the answer looks quiet tedious when i do it this way, i notice here that there is a special case for $\dfrac{1}{z^4+1}$, is there perhaps something similar for this -Thanks.

Community
  • 1
HappyFeet
  • 736
  • Not that it is necessary, but the change of variable $x=\sqrt{2},t$ transforms the problem into one of the problems linked to. – André Nicolas Dec 26 '14 at 06:36

1 Answers1

1

The roots of $z^4+4=0$ are $4^{1/4}e^{ik\pi/4}$ for odd $k$. This turns out to be the four numbers $\pm1\pm i$

Empy2
  • 52,372