Prove that for all non-negative integers $m,n$, $\frac{(2m)!(2n)!}{m!n!(m + n)!}$ is an integer.
There is a answer given here to this question here.
I've seen how it can be proven using recurrence equations as well. When I was trying to solve this problem I was looking to represent it as the number of ways of counting something. Can anyone give such an example, thus proving the question another and very natural way?
Following I. Gessel, let's denote $\frac{(2m)!(2n)!}{m!n!(m + n)!}$ by $S(n,m)$ and call them super Catalan numbers.
In aforementioned paper Gessel proves Szily's identity: $$ S(m,n)=\sum_k(-1)^k\binom{2m}{m+k}\binom{2n}{n-k} $$ (it follows almost immediately e.g. from $(1+x)^{m+n}(1-x)^{m+n}=(1-x^2)^{m+n}$). Now, recall that without signs RHS is a Vandermonde convolution: $$ \sum_k\binom{2m}{m+k}\binom{2n}{n-k}=\binom{2(n+m)}{n+m}. $$ So $S(n,m)$ counts lattice paths from $(0,0)$ to $(n+m,n+m)$ with some signs (determined by the height of a path after first $2m$ steps).
Whether this combinatorial enough can, of course, be debated...
Introduction: The MO link provided by @JoeJohnson in the comment section clearly indicates that it is a tough problem to find a combinatorial interpretation for the positive integers \begin{align*} S(m,n)=\frac{(2m)!(2n)!}{m!n!(m+n)!}\tag{1} \end{align*} Ira Gessel introduced for $S(m,n)$ the term Super Catalan Numbers in his paper about Super Ballot Numbers from 1992. See the answer from @GrigoryM providing some information about it. In this paper (section 6) Ira Gessel also introduces the identity
\begin{align*} \sum_{n\geq 0}2^{p-2n}\binom{p}{2n}S(m,n)=S(m,m+p)\qquad\qquad p\geq 0\tag{2} \end{align*}
which together with the initial value $S(0,0)=1$ and the symmetry $S(m,n)=S(n,m)$ shows that $S(m,n)$ is a positive integer.
Alas, he also writes that it remains to be seen whether (2) can be interpreted in a natural way.
In 2004, twelve years later(!) we can read in another paper by Ira Gessel in the introductory section:
An intriguing problem is to find a combinatorial interpretation to the super Catalan numbers.
Conclusion: A combinatorial intepretation for $S(m,n)$ is a tough problem.
Nevertheless I would like to give at least a proposal or an invitation to the reader to look for a combinatorial interpretation in terms of lattice paths.
Observe, that $S(m,n)$ can be written as
\begin{align*} S(m,n)=\frac{\binom{2m}{m}\binom{2n}{n}}{\binom{m+n}{n}}\tag{3} \end{align*}
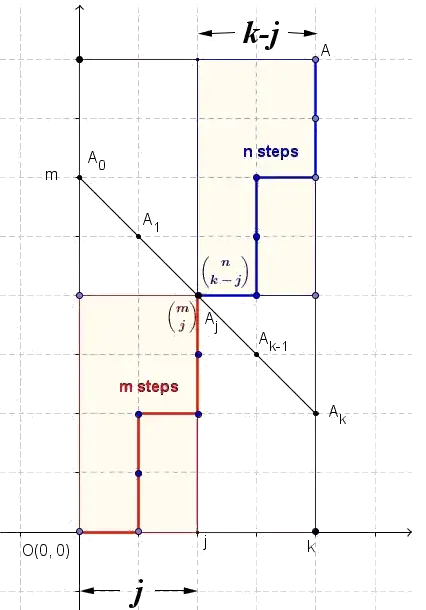
Interpreting this fraction in terms of lattice paths, containing solely of $(1,0)$-steps in $x$-direction and $(0,1)$-steps in $y$-direction, we can see
the numerator \begin{align*} \binom{2m}{m}\binom{2n}{n}\tag{4} \end{align*} counts the number of paths of length $2m+2n$ from $(0,0)$ to $(m+n,m+n)$ passing through the point $(m,m)$ or equivalently it counts the number of paths from $(0,0)$ to $(m,m)$ times the number of paths from $(0,0)$ to $(n,n)$.
On the other hand
the denominator \begin{align*} \binom{m+n}{m}\tag{5} \end{align*} counts the number of paths of length $m+n$ from $(0,0)$ to $(m,n)$ or symmetrically the number of paths from $(0,0)$ to $(n,m)$.
Idea: Since we know the fraction in (3) is a positive integer, it should be possible to find a mapping from each of the $\binom{m+n}{m}$ paths in (5) to a set of paths corresponding to the interpretation in (4).
For each of the $\binom{m+n}{m}$ paths this mapping should partition the $\binom{2m}{m}\binom{2n}{n}$ paths into equally sized classes and the challenge is to find a natural mapping for this partition.
Let's look at a simple example with $m=2,n=1$ and encode paths using $0$ for a step in $x$-direction and $1$ for a step in $y$-direction. We observe
\begin{array}{cccc} \binom{4}{2}=6&\binom{2}{1}=2&\qquad&\binom{3}{1}=3\\ \hline 0011&01&\qquad&001\\ 0101&10&\qquad&010\\ 0110&&\qquad&100\\ 1001&&\qquad&\\ 1010&&\qquad&\\ 1100&&\qquad&\\ \end{array}
For each of the $\binom{m+n}{m}=\binom{3}{1}=3$ paths $001,010$ and $100$ we have to find a class containing 4 pairs of paths from $$\{0011,0101,0110,1001,1010,1100\}\times\{01,10\}$$ providing us with a natural combinatorial interpretation. At the time I wasn't able to find one, although I'm pretty sure that the information is properly encoded within these paths.
One idea was to view the $\binom{2m}{m}$ paths as part of a square grid in the $(x\times y)$-plane and the $\binom{m+n}{m}$ paths within a rectangular grid of length $m$ and height $n$ as part of a $(x\times z)$-plane. This way they form two faces of a rectangular solid and the paths are projections of an area within this solid to the faces. But I couldn't find a proper interpretation this way.
So, I invite the reader to do a small meditation exercise about the following problem:
Challenge: Imagine the $\binom{2m}{m}$ paths are part of an $m\times m$ grid within a $(u_1\times u_2)$-plane and the $\binom{2n}{n}$ paths are part of an $n \times n$ grid within a $(v_1 \times v_2)$-plane. Find a mapping or decipher the information encoded in the $\binom{m+n}{m}$ paths which are part of a $m \times n$ grid in a $(w_1 \times w_2)$-plane resulting in a naturally, equally sized partitioning of the $\binom{2m}{m}\binom{2n}{n}$ paths.
Following from Grigory M's advice here is a way of interpreting these super catalan numbers as counting lattice paths. We also use part of a proof by Vladimir Nikolin when we deal with the Vandermonde Convolution Formula and Szily's identity.
Szily's identity is proven by equating the $x^{2m} $coefficient in the following expression $(1+x)^{m+n}(1-x)^{m+n}=(1-x^2)^{m+n}$ and then multiplying both sides by $\frac{(-1)^m(2m)!(2n)!}{(m+n)!^2}$
We get $$ S(m,n)=\sum_k(-1)^k\binom{2m}{m+k}\binom{2n}{n-k} $$
This shows that this expression we are dealing with is an integer. It even seems to me like this is close enough to counting something, the number of ways of picking 1s from bracket expansions multiplied by a constant or something. But we can do better.
Grigory M suggested considering the Vandermonde convolution formula; $$ \sum_k\binom{2m}{m+k}\binom{2n}{n-k}=\binom{2(n+m)}{n+m}. $$
where the sum is over all k.
This identity can be rewritten as $$ \sum_{k=0}\binom{2m}{k}\binom{2n}{m+n-k} $$ by letting m+k go to k
Our super catalan expression is transformed into $$ S(m,n)=\sum_{k=0}(-1)^{k-m}\binom{2m}{k}\binom{2n}{m+n-k} $$
Now consider the following proof of the Vandermonde convolution formula; The number of paths in a lattice from the origin to a point A(m+n, m+n) taking only up and right steps is $\binom{2(m+n)}{m+n}$ (choosing which m+n steps are up steps in the 2(m+n) steps getting there)
Consider the following approach to counting the number of ways; Look at the line x + y = 2m
(the diagram is depicting the case of m instead of 2m)
(source: cut-the-knot.org)
Each path crosses the line at a unique point $A_j$
There are $\binom{2m}{k}$ ways to get to $A_j$
Then there are $\binom{2n}{m+n-k}$ moves left to choose to get to A(m+n, m+n).
So there are $\binom{2m}{k}$$\binom{2n}{m+n-k}$ paths that cross through $A_j$
Summing over all j gives our Vandermonde identity.
Now if we look at our most recent expression for these super catalan numbers we see that it is just counting the number of paths from the origin to A(m+n, m+n) that go through an even $A_i$ minus the number that go through an odd $A_i$ or vice versa depending on the parity of m. We have interpreted this expression as counting something. It follows that it's an integer.
Although I can no longer see at all why it has to be a positive integer, but sure hey, that's what the original expression is for.
What about the following interpretation : I have a box of 2m elements, a box of 2n elements, and I want to count the number of ways of picking m elements from the first box and n elements from the second one without order. There are $\frac{(2n)!}{n!}$ ways of picking from the 2n box (with ordering), $\frac{(2m)!}{m!}$ ways of picking from the 2m box (with ordering), and since I don't care about the ordering of the elements, all is left to do is to divide my (n+m)!, the number of ways to order those n+m elements. In the end we get $$\frac{(2n)!(2m)!}{(n+m)!n!m!}$$ which must be an integer.
