7

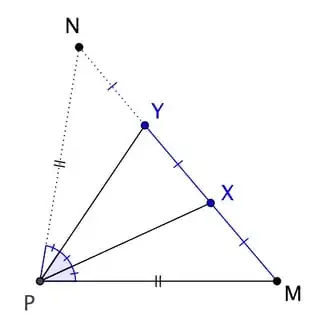
In this Numberphile video it is stated that trisecting an angle is not possible with only a compass and a straight edge. Here's a way I came up with:

Let the top line be A and bottom line be B, and the point intersecting P.
1. Use the compass and pick any length. Draw a point M n units from P on A. Use the compass again to draw a point N n units from P on B.
2. Connect M and N.
3. Since we know how to trisect a line, we can trisect it and get 3 equal distance line segments with 2 points in between.
4. Connect the 2 points to the point P.
5. Done.

This seems to work for all angles that are not 0 or 180 degrees. Given that it is proven that it's not possible to trisect an angle with only compass and a ruler without marks, something must have been wrong in my steps but I can't see any. Where is my mistake?

David Richerby
  • 2,480
Derek 朕會功夫
  • 703

3 Answers3

10

Let $X$ and $Y$ be the two points you added to $\overline{MN}$, as shown.

enter image description here

Consider $\triangle PMY$. Assuming your trisection construction to be valid, $\overline{PX}$ must bisect $\angle MPY$. By the Angle Bisector Theorem, we have $$\frac{|\overline{PM}|}{|\overline{PY}|} = \frac{|\overline{XM}|}{|\overline{XY}|} = 1$$ so that $\overline{PM}\cong\overline{PY}$. By the same logic, $\overline{PN}\cong\overline{PX}$. Thus, $M$, $N$, $X$, $Y$ are all equidistant from $P$.

See the problem?

Blue
  • 83,939
7

If $\angle APB= \alpha$, then middle angle (middle part) will have measure $$ \beta = 2\arctan \left(\frac{\tan(\alpha/2)}{3}\right) {\Large\color{red}{\ne}} \dfrac{\alpha}{3}. $$

A few examples: \begin{array}{|c|c|c|} \hline \alpha & \beta & error\\ \hline 3^\circ & 1.000203^\circ & 0.0203\%\\ 6^\circ & 2.001626^\circ & 0.0813\%\\ 9^\circ & 3.005494^\circ &0.183\%\\ \hline 30^\circ & 10.207818^\circ & 2.078\%\\ 60^\circ & 21.786789^\circ & 8.933\%\\ 90^\circ & 36.869897^\circ & 22.899\%\\ \hline \end{array}

When angles are small, then this method gives not bad approximation, but it isn't the exact way of trisection.

Oleg567
  • 17,740
5

Let your angle be almost 180 degrees, so your two lines are almost coincident. The line $MN$ is also almost parallel to the lines, and trisecting that segment leads to very unequal "thirds" of the angle.

Victor Liu
  • 3,771
  • They are almost "parallel", but they aren't. With great precision trisecting the angle is still possible with this method. – Derek 朕會功夫 Dec 13 '14 at 08:12
  • 4
    No, using your method, the middle "third" is always larger than the outer two "thirds". The arc length of the circular segments are not proportional to the pieces of the chord. – Victor Liu Dec 13 '14 at 08:13
  • I see what you mean now. Since the distance from the middle point to the middle segment is way closer than the other two, the angle in between would be much greater than the other two, so this method only works for small angles. Thanks. – Derek 朕會功夫 Dec 13 '14 at 08:19
  • 2
    @Derek朕會功夫 This does not work for small angles either. – peterwhy Dec 13 '14 at 08:29
  • 1
    @peterwhy - Oh by work I mean a good enough approximation... like how $y=x$ is a "good enough" approximation of $y=\sin{x}$ if $x$ is small. – Derek 朕會功夫 Dec 13 '14 at 10:24
  • An initial 135 degrees angle would also demonstrate the problem quite well. The resulting 3 angles would not be 45 degrees and it's easy to check visually (adding 2 of them would not be equal to 90 degrees) – ypercubeᵀᴹ Dec 13 '14 at 13:52
  • @Derek朕會功夫: When people say that trisecting an angle is impossible, they're talking about doing it exactly. It's always possible to come up with approximate trisections that only use straightedge and compass, that come as close as you like to being a genuine trisection... – Micah Dec 13 '14 at 17:35