Nice proof that $\mathbb{Z}[\sqrt{6}]$ is a Euclidean domain wrt absolute norm map

Question

I know that $\mathbb{Z}\left[\sqrt{6}\,\right]$ is a Euclidean domain with respect to the absolute valued norm map $x+y\sqrt{6} \mapsto |x^2-6y^2|$. I think I proved this result with some common techniques, but the proof is a bit sloppy and it requires a lot of cases. (Basically, I checked that for every $z \in \mathbb{Q}(\sqrt{6})$ there is $\gamma \in \mathbb{Z}[\sqrt{6}]$ such that $|N(z-\gamma)|<1$.)

Does there exist a short proof for this result, with less cases or a more, say, enlightening method?

Many thanks.

Isn't the usual method to draw parallelograms in the complex plane and show that the distance to a vertex is bounded sufficiently well? — Nishant, Nov 26 '14 at 21:59
I don't know, can you give me a reference or explain it to me? :-) — Jef, Nov 26 '14 at 22:00
Oh never mind, I thought it was $\sqrt{-6}$...your ring is contained in the real numbers so my suggestion doesn't work. — Nishant, Nov 26 '14 at 22:03
I've been thinking about this question but I'm not ready to set down an answer. If I were to pull it off, I think I'd probably need three cases: $x = 0, y \neq 0$; $x \neq 0, y = 0$; $x \neq 0, y \neq 0$. — Robert Soupe, Dec 01 '14 at 03:08
Oh, but if these are the only ones, then it would be really nice! :-) — Jef, Dec 01 '14 at 13:39
http://math.stackexchange.com/questions/124484/show-mathbbz-sqrt6-is-a-euclidean-domain — Jacob Bond, Dec 01 '14 at 17:10
As I think more about it, I think my cases would be, given ${m, n} \in \mathbb{Z}[\sqrt{6}]$, more like this: that both $m$ and $n$ are good ol' integers; both $m$ and $n$ have "radical parts" only; $m$ has a "whole part" and a "radical part" but $n$ has only a "radical part"; etc. — Robert Soupe, Dec 04 '14 at 04:04
some ideas maybe here: http://www.math.uconn.edu/~kconrad/blurbs/ringtheory/euclideanrk.pdf — cactus314, Dec 04 '14 at 12:28

score 3 · Accepted Answer · edited Apr 13 '17 at 12:19

this question has been answered here: https://math.stackexchange.com/a/124573/4997

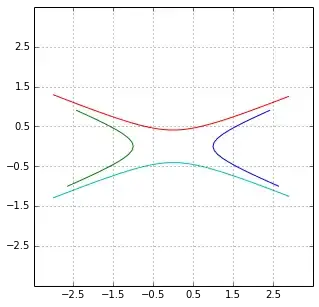
enter image description here

this is a picture of one of the "starfish" - a region bounded by two hyperbolas.

Reading this review by Franz Lemmermeyer, The Euclidean Algorithm in Algebraic Number Fields

Theorem The rings $\mathcal{O}_{\mathbb{Q}[\sqrt{d}]}$ are norm-Euclidean if and only if $m \in \{ 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57, 73\}$.

Fortunately, in the internet age. Oppenheim's 1934 paper Quadratic Fields with and Without Euclid's Algorithm is online. The preview page is all you need.

Forget about the case $m \equiv 1 \mod 4$ (since $m = 6$), we want to find $m$ such that for any rational point $(a,b)$ we can find $(x,y) \in \mathbb{Z}^2$ such that $|(x-a)^2 - m (y-b)^2 | < 1 $

Oppenheim proceeds by process of eliination: if we can find $(a,b) \in \mathbb{Q}^2$ such that for all integers $(x,y) \in \mathbb{Z}^2$ either

$(x-a)^2 - m (y-b)^2 \geq 1 $
$m (y-b)^2 - (x-a)^2 \geq 1 $

Then we have ruled out the possibility of $m$ as a Euclidean domain (with this particular norm). This then becomes a quadratically constrained quadratic programming problem. Let's assume $0 < a,b < \tfrac{1}{2}$.

Examining the constraints around the points $(0,0), (1,0), (-1,0)$ one can show $mb^2 \geq 1 + (1 + a)^2 \geq 2$ and $m \geq 8$.

$m = 2,3,\mathbf{6},7$ work.

To get $m = 5,13,17,21,29$, a modified Euclidean algorithm gives the same constraints with norm $|(x + \tfrac{1}{2}y)^2 - \tfrac{1}{4}my^2 | $

I read this proof and would like to understand better how these constraints dictate problems with factorization.

It's common to talk about $|x^2 - 6y^2 |< 1$ as a sphere even though the interior of a hyperbola. One could solve Pell's equation $x^2 - 6y^2 = 1$ by finding the continued fraction expansion of $\sqrt{6}$, which is periodic. Maybe we can use continued fractions to solve $|(x-a)^2-6(y-b)^2 |< 1$. — cactus314, Dec 04 '14 at 15:08
A modern device for quadratic forms is the topograph as discussed by Ch 2 of Topology of Numbers by Allen Hatcher — cactus314, Dec 04 '14 at 15:28

Nice proof that $\mathbb{Z}[\sqrt{6}]$ is a Euclidean domain wrt absolute norm map

1 Answers1