0

A Mobius transformation of the plane takes $z \mapsto \frac{az+b}{cz+d}$. These are known to take circles to circles, but given an explicit circle, how do we compute the radius.

Let's parameterize our circle by $z(t) = z_0 + r e^{2\pi i n t}$. What is the radius and center of the image circle?

$$ \frac{a\,z(t)+b}{c\,z(t)+d}$$

I am looking for a computational proof that the image is a circle so I can find the (Euclidean) radius and center.

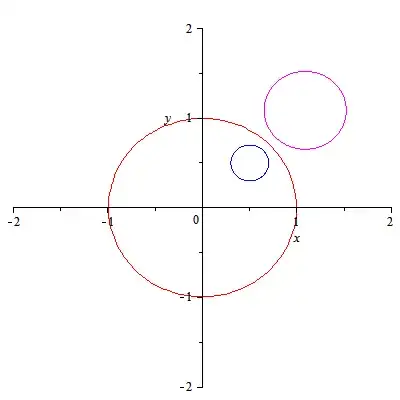
From Wikipedia

Source: Wikipedia

In my application, I have an approximate circle $\{ z_0 + e^{2\pi i n t}: t \in \frac{1}{N}\mathbb{Z} \}$ where $N$ is a large number. If we act the Mobius transformation pointwise, these spaces will no longer be evenly spaced out. So I decided it's better to compute the Euclidean center and radius if possible.

cactus314
  • 25,084
  • http://math.stackexchange.com/questions/360954/when-we-have-circle-in-hyperbolic-plane-what-is-the-center-and-radius-of-this-ci – cactus314 Nov 19 '14 at 16:56
  • See https://math.stackexchange.com/questions/3068729/what-is-the-radius-and-center-of-the-image-of-z-1-under-fz-frac3z2/3550469#3550469 – Stéphane Laurent Feb 18 '20 at 12:33

1 Answers1

2

I'm not sure this will fully satisfy you but I might as well write it down.

Instead of centering your original circle $\Gamma$ on the origin, you can center your Mobius transform so that it becomes $z\mapsto \frac{a}{z}+b$. This reduces the problem to finding the image of a given circle under complex inversion, which is much easier.

Your image circle $\Gamma'$ is the symmetric reflection of the image of $\Gamma$ under $\phi:z\mapsto \frac{1}{\bar{z}}$. It is easily checked that $\phi$ is the transformation of $\mathbb{R}^{2}$ that associates to a vector $x$ the vector $\frac{x}{||x||^{2}}$. By a symmetry argument (look at the tangents to $\Gamma$ passing throught the origin), the origin, the center of $\Gamma$ and the center of $\Gamma'$ are colinear. This allows you to calculate your radius and your center.

With all this you can do the computations, but I don't really feel like explicitly writing them down... You can also turn the above discussion into a proof that the image is indeed a circle: it is enough to prove that $\phi$ sends circles not passing through the origin into other circles, and this can be done with elementary geometry (anti-similar triangles) by showing that $\phi$ preserves angles between three points.

Sergio
  • 3,519
  • translation clearly preserves the radius and center. I am wondering what $z \mapsto \frac{1}{\overline{z}}$ does to arbitrary circles. – cactus314 Nov 17 '14 at 03:22
  • $z\mapsto \displaystyle\frac{1}{\bar{z}}$ is the composition of $1/z$ with an axial symmetry, so it sends circles passing through the origin into lines and other circles into other circles. Do you want a proof of the fact that it sends circles into circles ? – Sergio Nov 17 '14 at 17:23
  • I need a way to find the Euclidean center of that circle – cactus314 Nov 18 '14 at 12:33
  • Let $C,C'$ be the centers of $\Gamma, \Gamma'$. If $A$ and $B$ are the intersection points of $(OC)$ with $\Gamma$ (where $O$ is the origin), then $C'=\frac{1}{2}(\phi(A)+\phi(B))$. – Sergio Nov 18 '14 at 20:40