Suppose that an ellipse is rolling along a line. If we follow the path of one of the foci of the ellipse as it rolls, then this path formes a curve - namely an undulary. Now consider the following diagram
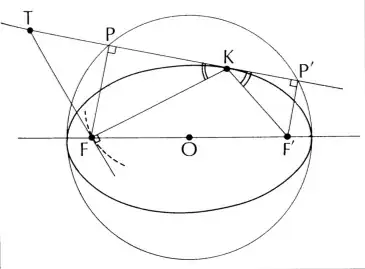
The points $F$ and $F'$ are the forci of the ellipse, which is rolling along the line $KT$. The line $FT$ is the tangent to the curve traced out by $F$. Now the following folds:
$FT$ is is perpendicular to $FK$, so the normal to the locus of $F$ passes through $K$.
Why is this always the case? I read this in 3 several books, but every time without a proof. Is it that obvious? Can anyone explain it or give a proof/source?
Best regards!