Jacobi Triple Product Question.

Question

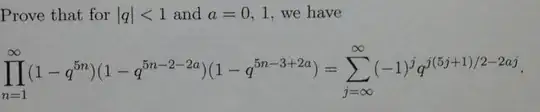
Here is the question I am stuck on..

Sorry if it is hassle viewing the image but my fluency with MathJax is quite poor. I have seen some examples of Jacobi triple product already. Does the one below represent The second Ramanujan Identity? And how would you go about converting this product to the sum. Any help at all would be appreciated.

do you need more information on the Jacobi triple product and such? — Avitus, Nov 11 '14 at 09:02

score 2 · Accepted Answer · edited Apr 13 '17 at 12:21

2

The formula you write is the Jacobi triple product identity (JTPI)

$$\prod_{i=1}^\infty (1-q^{2n})(1+q^{2n-1}z)(1+q^{2n-1}z^{-1})=\sum_{j=-\infty}^\infty q^{n^2}z^n$$

under the substitutions

$$q=q^{\frac{5}{2}}$$

and

$$z=-q^{\frac{1}{2}-2a}.$$

The proof of JTPI can be easily found on textbooks.

For more explanations and insights I refer to the excellent answers in this thread.

edited Apr 13 '17 at 12:21

Community

1

answered Nov 06 '14 at 17:19

Avitus

14,348
1
31
52

Jacobi Triple Product Question.

1 Answers1