Explanation regarding statement of the Implicit Function Theorem .

Question

My notes define the implicit function theorem as follows :

Let $E$ be an open set in $\mathbb R^{n+m}$ and $f\in C^1(E,\mathbb R^n)$ such that for some $f(a,b)=0$ for some $(a,b)\in E$ .
Let $A$ be the jacobian of $f$ at $(a,b)$. Then $A$ is an $n+m\times n$ matrix.
Write $A=[A_1~~ A_2]$ . Assume that $A_1$ is invertible.

Thus $f'(a,b)(h,k)=A$$ \left[ \begin{array}{ccc} h \\ k \end{array} \right]$ $=A_1h+A_2k,$ for any $(h,k)\in \mathbb R^{n+m}$ .Then there are open sets $U\subseteq \mathbb R^{n+m}$ and $W\subseteq R^{m}$ with $(a,b)\in U$ and $b\in W$ such that to every $y\in W$ ,there corresponds a unique $x$ such that $(x,y)\in U$ and $f(x,y)=0$
Thus this defines a map $y\mapsto x$ .If this map is defined to be $g(y)$ ,then $g\in C^1(W,\mathbb R^n)$ , $g(b)=a$ ,for all $y\in W :$
$$f(g(y),y))=0 ~~and~~J_g(b)=-A_1^{-1}A_2$$

Although I understood the intution to this theorem in $2$-D using the answer posted by @Fabian in What is the 'implicit function theorem'? I can't understand this definition in my notes at all , it seems to be confusing to me .
Can anyone explain this definition in my notes to me in a very simple to understand language of what it means to say ...

Answer 1

The way I think and teach about IFT is the following. Largely geometric/visual, so may be not to everybody's liking.

Let us ignore the separation into $(h,k)$ parts. Just consider a point $\mathbf{p}\in\Bbb{R}^{n+m}$. Let $f_1,f_2,\ldots,$ be some functions from a neighborhood of $\mathbf{p}$ to the reals, all vanishing at $\mathbf{p}$. Let us select a finite non-empty subset $S$ of those functions, and let $V(S)$ be the set of common zeros of the functions in $S$. We call a vector $\vec{w}$ a tangent of $V(S)$ at $\mathbf{p}$, if there exists a differentiable path $\gamma:(-a,a)\to V(S)$ for some $a>0$ such that $\gamma(0)=\mathbf{p}$ and $\gamma'(0)=\vec{w}$.

Implicit function theorem states (essentially) that if the gradients $\nabla f(\mathbf{p}), f\in S,$ are linearly independent, then the tangent vectors of $V(S)$ at $\mathbf{p}$ form a linear subspace $L$ of $\Bbb{R}^{n+m}$. Moreover that subspace consists of the vectors orthogonal to the gradients $\nabla f(\mathbf{p}), f\in S$. The tangent space $T(S,\mathbf{p})$ of $V(S)$ at $\mathbf{p}$ is translated to pass through $\mathbf{p}$, so it is the coset of a linear subspace $T(S,\mathbf{p})=L+\mathbf{p}$

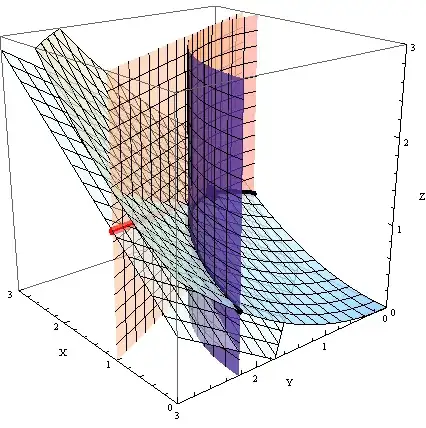
In the above figure the point $\mathbf{p}$ is the black dot (barely visible through the semi-opaque surfaces). The set $S$ consists of two functions, and their zero sets are the section of a vertical cylindrical tube (quarter of a tube to be more precise) and that light blue slightly bent surface. The vertical plane and th slanting plane are their respective tangent planes at $\mathbf{p}$. The intersection $V(S)$ is that solid black curve, and its tangent space is that red line that is also the intersection of the two tangent planes.

This brings us to a following one-line summary of IFT:

The tangent space of the intersection is the intersection of the tangent spaces.

What does that got to do with the formula for the partial derivatives of the "coordinates to be solved" with respect to the "coordinates viewed as independent variables"?

Well. When those gradients are linearly independent, then the above description of the tangent space tells that it consists of solutions of an underdetermined system of linear equations. Finding its general solution was done in linear algebra. For example we remember that we can solve a subset of $m$ coordinates from those $m$ linear equations iff the corresponding $m\times m$ matrix consisting of the relevant columns is invertible.

What IFT says is that the same holds locally in the differentiable (but no longer linear) case. Furthermore, all those partial derivatives at $\mathbf{p}$ are coded into the equation of that tangent plane, which can be viewed as the graph of an affine linear function from $\Bbb{R}^n$ to $\Bbb{R}^m$.

Answer 2

More or less the intuitive idea is:

If you have a function $f$ with domain $\mathbb{R}^{n+m}$, that is $n+m$ variables satisfying the hypotheses in the theorem then you can "get rid" of the first $n$ variables and Write it only as a function of $m$ variables: that is there exists a function $g$ such that in a neighbourhood you can Express $f$ With less variables: $$f(x_1,\dots, x_n, x_{n+1}, \dots,m) = f(g(x_{n+1},\dots, x_m), x_{n+1},\dots, x_m).$$

If the dimension is $2$ and $n=1$, $m=1$ then you can write $f(x,y) = f(g(y),y)$ just as a function of one variable. If for example, the dimension is $3$ and $n=2$, $m=1$ under the hypotheses of the theorem you may express $f(x,y,z)=f(g(y,z),z)$, and so on.