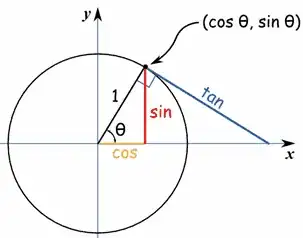
I am having the hardest time figuring out what sin and cos are doing when you enter in calculator.
What I do understand about them
1) They are both essentially finding the max and min values for their respective axis. cos being x and sine being y.
-this makes PERFECT sense. Yay!
2) You can find what other lengths of a triangle are. (value(sin(theta)) (value(cos(theta)) **most cases theta needs to be in radians i understand that.
-this makes sense. Yay!
Ok, so what the heck is going on when you do sin($\pi$/6). How does that equal 1/2? I understand that basically the sine of $\pi$/6 (y min and max) would be 1/2, ok but why? when you do cos(0), x = 1 because r = 1 (why is r = 1?). This is where I am confused. Again, I can do this stuff on calculator but I am a programmer and if things don't make sense my head spins and I need to understand what is going on.