Why removing rows with NA values from the majority class improves model performance

Question

I have an imbalanced dataset like so:

df['y'].value_counts(normalize=True) * 100

No     92.769441
Yes     7.230559
Name: y, dtype: float64

The dataset consists of 13194 rows and 37 features.

I have tried numerous attempts to improve the performance of my models by oversampling and undersampling to balance the data, One Class SVM for outlier detection, using different scores, hyperparametre tuning, etc. Some of these methods have improved the performance slightly, but not as much as I would like:

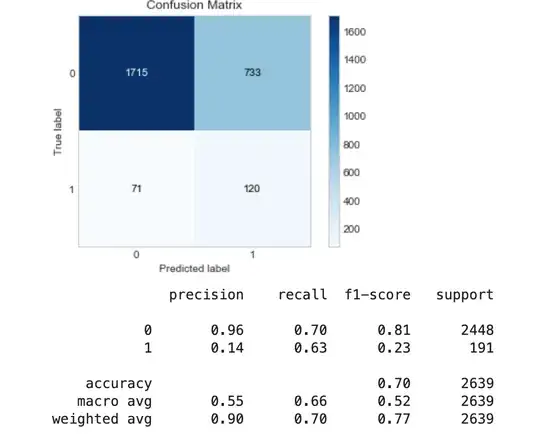
Applying RandomUnderSampling:

from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=42)
X_train_rus, y_train_rus = rus.fit_resample(X_train, y_train)
Define and fit AdaBoost classifier using undersampled data
ada_rus = AdaBoostClassifier(n_estimators=100, random_state=42)
ada_rus.fit(X_train_rus,y_train_rus)
y_pred_rus = ada_rus.predict(X_test)
evaluate_model(y_test, y_pred_rus)

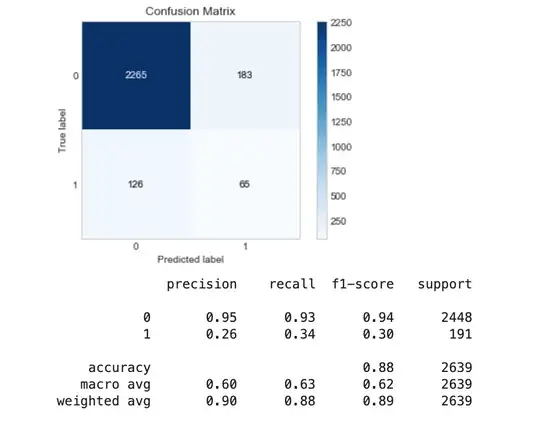
Using Oversampling techniques such as SMOTE:

# SMOTE
from imblearn.over_sampling import SMOTE
upsample minority class using SMOTE
sm = SMOTE(random_state=42)
X_train_sm, y_train_sm = sm.fit_sample(X_train, y_train)
Define and fit AdaBoost classifier using upsample data
ada_sm = AdaBoostClassifier(n_estimators=100, random_state=42)
ada_sm.fit(X_train_sm,y_train_sm)
y_pred_sm = ada_sm.predict(X_test)
compare predicted outcome through AdaBoost upsampled data with real outcome
evaluate_model(y_test, y_pred_sm)

I then decided to attempt removing rows with missing data from samples from the majority class as I saw this in an article. I did this gradually by increasing the threshold (thresh) parameter in pandas dropna function, and each time I removed more rows, the performance improved. Finally, I removed all rows from the majority class with missing data like so:

df_majority_droppedRows = df.query("y == 'No'").dropna()
df_minority = df.query("y == 'Yes'")
dfWithDroppedRows = pd.concat([df_majority_droppedRows, df_minority])
print(dfWithDroppedRows.shape)

(1632, 37)

This reduced the number of rows I have dramatically down to 1632 and changed the distribution in the target variable such that what was perviously the minority class('Yes') was now the majority class:

Yes    58.455882
No     41.544118
Name: y, dtype: float64

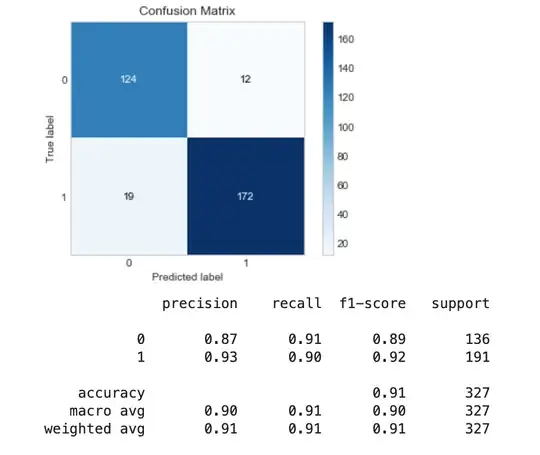
Testing the model, I found it performed best, with high recall and precision values.

So my questions are,

1. Why did this method outperform other oversampling and undersampling techniques?

2. Is it acceptable that what was previously a minority class is now the majority class or can this cause overfitting?

3. Is it realistic to build a model that relies on input with no missing data for the majority class samples?

EDIT

In response to the questions in the comment by @Ben Reiniger:

• I dealt with the missing values like in the data by using KNNImputer for numeric data and SimpleImputer for categorical data like so:

def preprocess (X):
    # define categorical and numeric transformers
    numeric_transformer = Pipeline(steps=[
        ('knnImputer', KNNImputer(n_neighbors=2, weights="uniform")),
        ('scaler', StandardScaler())])
categorical_transformer = Pipeline(steps=[
    ('imputer', SimpleImputer(strategy='constant', fill_value='missing')),
    ('onehot', OneHotEncoder(handle_unknown='ignore'))])

preprocessor = ColumnTransformer(transformers=[
    ('cat', categorical_transformer, selector(dtype_include=['object'])),
    ('num', numeric_transformer, selector(dtype_include=['float64','int64']))
])

X = pd.DataFrame(preprocessor.fit_transform(X))
return X 

• After dropping rows, I defined the feature of matrix and the target, preprocessed and then split the data, like so:

# make feature matrix and target matrix
X = dfWithDroppedRows.drop(columns=['y'])
y = dfWithDroppedRows['y']
encode target variable
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)
preprocess feature matrix
X=preprocess(X)
Split data into training and testing data
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.2, random_state=42)

• Finally, to calculate if the missing values are identically distributed (originally) in the two classes, I ran the following

np.count_nonzero(df.query("y == 'No'").isna()) / df.query("y == 'No'").size

0.2791467938526762

np.count_nonzero(df.query("y == 'Yes'").isna()) / df.query("y == 'Yes'").size

0.24488639582979205

So the majority class has about 28% missing data and the minority class has about 25% missing data.

Answer 1

You have a combination of two problems in your data:

• imbalance
• missing values

In your experiments there's a confusion about what the true distribution of the data is (or should be): either the "real data" is 97% no, or the "real data" is after removing missing values in which case it's almost balanced. It's very important to decide this based on the problem that you're trying to solve: "in production", does the model have to produce a prediction for every instance even if it has missing values? If yes the true distribution is 97% no (original problem). If no, then the model only predicts for "complete" instances, i.e. many instances are discarded due to missing values (and this happens much more often with "no").

This is a crucial point because whichever way you train the model, it should be evaluated on a test set which reflects the true distribution of the data.

I would assume that your real goal is to predict for every instance, i.e. you don't want to ignore instances even if they have missing values. I will try to address both options though:

• option A: real data is 97% no.
• option B: real data is 58% yes.

1. Why did this method outperform other oversampling and undersampling techniques?

The two methods were evaluated on two very different test sets, so the performance between them is simply not comparable.

• If the resampling experiments were properly evaluated on the original data (not resampled), then they provide you with a reliable estimate of the performance in option A.
• If the resampling experiments were (wrongly) evaluated on resampled data, then the difference is certainly due to the missing values, because imputing a very large proportion of the data causes a lot of noise. In this case the resampling experiments are neither valid for option A (wrong distribution in the test set) nor B (missing values in the test set).

2. Is it acceptable that what was previously a minority class is now the majority class or can this cause overfitting?

It depends which problem you're trying to solve:

• For the original problem "option A", no it is not acceptable to modify the distribution in the test set.
• For the new problem "option B", the majority class is "yes". The original data with 97% "no" is irrelevant.

3. Is it realistic to build a model that relies on input with no missing data for the majority class samples?

This is about specifying the exact problem you want to solve, that's for you to decide :)