How do I interpret my result of clustering?

Question

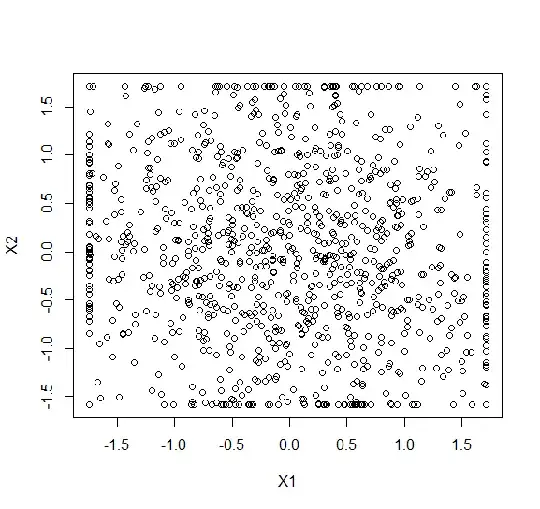
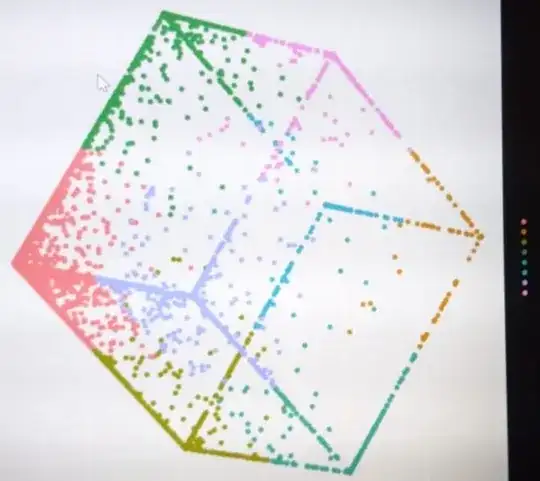
I am working on a clustering problem. I have 11 features. My complete data frame has 70-80% zeros. The data had outliers that I capped at 0.5 and 0.95 percentile. However, I tried k-means (python) on data and received a very unusual cluster that looks like a cuboid. I am not sure if this result is really a cluster or has something gone wrong?

The main reason for my worry, why is it looking like a cuboid and why are the axes orthogonal?

one thing to notice is that: I first reduced the dimensionality using PCA to two dimensions and performed clustering on the same and the plot here is on the 2-dim PCA data

Edit : I chose k using silhouette index in python.

Answer 1

K-means don't modify the underlying structure of your data. K-means will just provide the 'color' part of your graph.

To answer the question about why do you get a cuboid, it's because your underlying data are a cuboid. Not necessarily by construction, but that's what happen when you cap your data. As an exemple, look at the following code :

X1 = c(rnorm(1000))
X2 = c(rnorm(1000))
q95_1 = quantile(X1,0.95)
q95_2 = quantile(X2,0.95)
q5_1 = quantile(X1,0.05)
q5_2 = quantile(X2,0.05)
X1[X1>q95_1]=q95_1
X2[X2>q95_2]=q95_2
X1[X1<q5_1]=q5_1
X2[X2<q5_2]=q5_2
plot(X1,X2)

The code simulate two random gaussian and cap them at 5% and 95%.

this is what you get :

Notice the squaroid pattern ? This is why you get a cuboid in 3D.

Ps: I can't help but say that's what you get when you do k-means without properly looking at your variables (see: What value can I gain by doing exploratory data analysis on features (and thus data) before doing clustering? for an infinite loop).