Cross validation Vs. Train Validate Test

Question

I have a doubt regarding the cross validation approach and train-validation-test approach.

I was told that I can split a dataset into 3 parts:

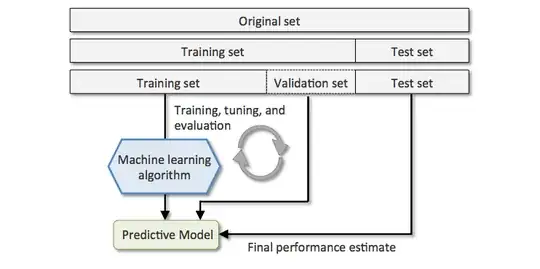
1. Train: we train the model.
2. Validation: we validate and adjust model parameters.
3. Test: never seen before data. We get an unbiased final estimate.

So far, we have split into three subsets. Until here everything is okay. Attached is a picture:

Then I came across the K-fold cross validation approach and what I don’t understand is how I can relate the Test subset from the above approach. Meaning, in 5-fold cross validation we split the data into 5 and in each iteration the non-validation subset is used as the train subset and the validation is used as test set. But, in terms of the above mentioned example, where is the validation part in k-fold cross validation? We either have validation or test subset.

When I refer myself to train/validation/test, that “test” is the scoring:

Model development is generally a two-stage process. The first stage is training and validation, during which you apply algorithms to data for which you know the outcomes to uncover patterns between its features and the target variable. The second stage is scoring, in which you apply the trained model to a new dataset. Then, it returns outcomes in the form of probability scores for classification problems and estimated averages for regression problems. Finally, you deploy the trained model into a production application or use the insights it uncovers to improve business processes.

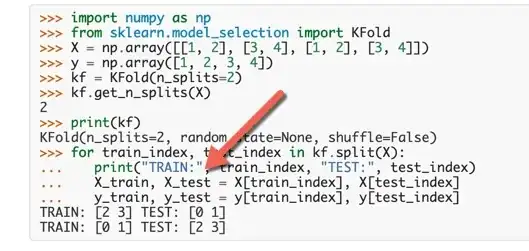
As an example, I found the Sci-Kit learn cross validation version as you can see in the following picture:

When doing the splitting, you can see that the algorithm that they give you, only takes care of the training part of the original dataset. So, in the end, we are not able to perform the Final evaluation process as you can see in the attached picture.

Thank you!

scikitpage

Answer 1

If k-fold cross-validation is used to optimize the model parameters, the training set is split into k parts. Training happens k times, each time leaving out a different part of the training set. Typically, the error of these k-models is averaged. This is done for each of the model parameters to be tested, and the model with the lowest error is chosen. The test set has not been used so far.

Only at the very end the test set is used to test the performance of the (optimized) model.

# example: k-fold cross validation for hyperparameter optimization (k=3)

original data split into training and test set:

|---------------- train ---------------------|         |--- test ---|

cross-validation: test set is not used, error is calculated from
validation set (k-times) and averaged:

|---- train ------------------|- validation -|         |--- test ---|
|---- train ---|- validation -|---- train ---|         |--- test ---|
|- validation -|----------- train -----------|         |--- test ---|

final measure of model performance: model is trained on all training data
and the error is calculated from test set:

|---------------- train ---------------------|--- test ---|

In some cases, k-fold cross-validation is used on the entire data set if no parameter optimization is needed (this is rare, but it happens). In this case there would not be a validation set and the k parts are used as a test set one by one. The error of each of these k tests is typically averaged.

# example: k-fold cross validation

|----- test -----|------------ train --------------|
|----- train ----|----- test -----|----- train ----|
|------------ train --------------|----- test -----|

Answer 2

@Louic is mostly right, but this thread is off on a few points:

1. Train/val/test is a form of cross-validation. The question is comparing two methods of CV: k-fold vs "hold out". Decent resource here to read up on the various approaches.

2. Using the test set for evaluation occurs prior to "finalizing" the model. You evaluate the model that was trained without the test set so that it is unbiased. You then discard that model and train a final model on all data (train+test+val). You consider the score you got from the test set to be an estimate of the final model. You do this because there is no other way to evaluate a model trained on all data, but this estimate is the best we can do (because the final model has more data, in theory the score would be slightly better than the estimate, but we'll never know but how much!). I would highly recommend reviewing Jason Brownlee's post on finalizing models, which I have found to be one of the few entry-level sources that's spot-on

3. K-fold will pretty much always be better than hold-out. This is because you take advantage of the power of resampling since the test set will never be truly representative of unseen data. In other words, you would have a distribution of scores if you repeated the train+val+test process with a different mix of the same data. K-fold is the acknowledgement of this, and when allows you to measure the variance of the scores in each fold to better understand your sampling schema. Think of 5-fold CV has just doing 20% test holdout 5 times to check out good your original split was. However, if you have enough data, the gains are not worth the extra computation and therefore hold out is sufficient.

Answer 3

@louic's answer is correct: You split your data in two parts: training and test, and then you use k-fold cross-validation on the training dataset to tune the parameters. This is useful if you have little training data, because you don't have to exclude the validation data from the training dataset.

But I find this comment confusing: "In some cases, k-fold cross-validation is used on the entire dataset ... if no parameter optimization is needed". It's correct that if you don't need any optimization of the model after running it for the first time, the performance on the validation data from your k-fold cross-validation runs gives you an unbiased estimate of the model performance. But this is a strange case indeed. It's much more comment to use k-fold cross validation on the entire dataset, and tune your algorithm. This means you lose the unbiased estimate of the model performance, but this is not always needed.

Answer 4

Excellent question!

I find this train/test/validation confusing (I've been doing ML for 5 years).

Who says your image is correct? Let's go to an ML authority (Sk-Learn)

In general, we do k-Fold on train/test (see Sk-Learn image below).

Technically, you could go one step further and do a Cross Validation on everything (train/test/validation). I've never done it though ...

Good luck!