How to use correct weights in linear regression model

Question

I'm trying to understand can we implement a simple linear regression model.

Let's say we are predicting price currencies. We want to know whether the currency will raise or not.

As i understand, we need to define two vectors for this:

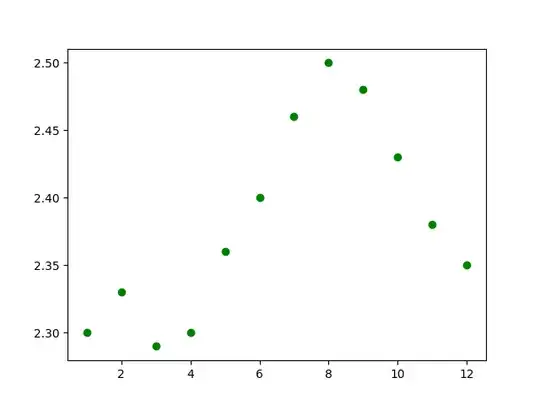
$x=[1,2,3,4,5,6,7,8,9,10,11,12]$ - months

$y=[2.30,2.33,2.29,2.30,2.36,2.40,2.46,2.50,2.48, 2.43,2.38,2.35]$ - average prices.

Let's plot this:

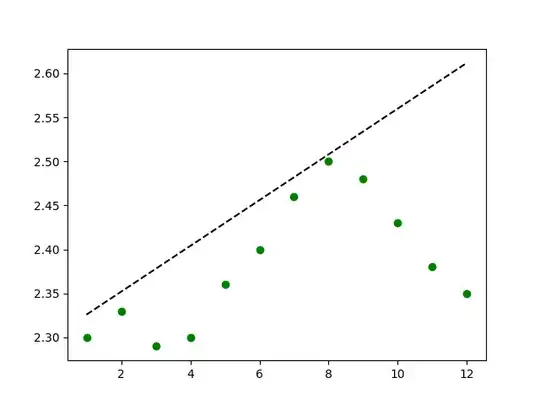
Before sigmoid separator, i will try a simple linear separator.

I'm guessing that at first, I need to choose some random slope (and bias will be the smallest scalar in vector).

$f(x) = 0.026x+2.3$

As we see, the separator is inaccurate, let's try the quadratic cost function at f(1):

$C = \frac{1}{N} \sum_{i=0}^{N}(\hat{y} - y)^2$

$C = \frac{1}{1} \sum_{i=0}^{1}(2.3259999999999996-2.30)^2=0.0006759999999999897$

It seems accurate in the beginning, but it gets worse as it progresses, so somehow i need to improve it.

From my knowledge, the next step is to find the derivative of the function.

Normally, gradient descent algorithm is used for this, but finding a slope of the tangent line is very easy here:

$\frac{dy}{dx} = 0.026$

What is the next step? How can i use this derivative to use proper weights to minimize the cost function?

Answer 1

You are correct for a linear separator line the derivative seems trivial. In this case gradient descent is not necessary because a closed form solution exists for the weights.

$w = (X^TX)^{-1}X^Ty$

We only use optimization techniques such as gradient descent for models where a closed form solution does not exist. However, if you perform gradient descent on the weights using the derivative and doing the following equation iteratively

$w^{new} = w^{old} - \nu \frac{dy}{dx}$

would yield the same result as the closed form solution. This is however very unnecessary when not necessary.