LeakyReLU vs PReLU

Question

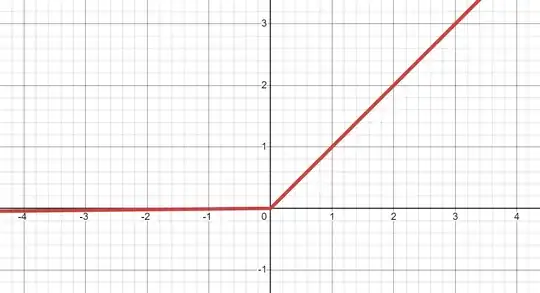
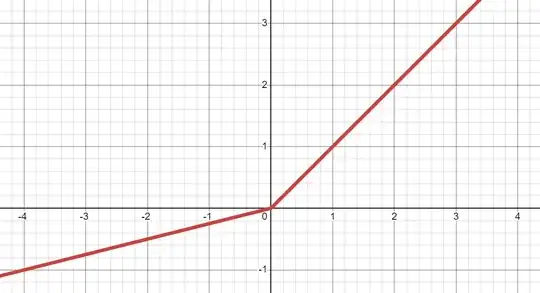
I thought both, PReLU and Leaky ReLU are: $$f(x) = \max(x, \alpha x) \qquad \text{ with } \alpha \in (0, 1)$$

Keras, however, has both functions in the docs.

Leaky ReLU

Source of LeakyReLU:

return K.relu(inputs, alpha=self.alpha)

Hence (see relu code): $$f_1(x) = \max(0, x) - \alpha \max(0, -x)$$

PReLU

Source of PReLU:

def call(self, inputs, mask=None):
    pos = K.relu(inputs)
    if K.backend() == 'theano':
        neg = (K.pattern_broadcast(self.alpha, self.param_broadcast) *
               (inputs - K.abs(inputs)) * 0.5)
    else:
        neg = -self.alpha * K.relu(-inputs)
    return pos + neg

Hence: $$f_2(x) = \max(0, x) - \alpha \max(0, -x)$$

Question

Did I get something wrong? Aren't $f_1$ and $f_2$ equivalent to $f$ (assuming $\alpha \in (0, 1)$?)

Answer 1

Leaky ReLUs allow a small, non-zero gradient when the unit is not active:

$$f(x) = \begin{cases} x & \text{if $x>0$}\\ \mathbf{0.01}x & \text{otherwise} \end{cases} $$

Parametric ReLUs take this idea further by making the coefficient of leakage ($0.01$ above) into a parameter that is learned along with the other neural network parameters:

$$f(x) = \begin{cases} x & \text{if $x>0$}\\ \alpha x & \text{otherwise} \end{cases} $$

Where $\alpha$ is the learnable parameter that is learned through gradient descent similar to the other neural network parameters such as weights and biases. Source

Answer 2

Pretty old question; but I will add one more detail in case someone else ends up here.

Motivation behind PReLU was to overcome shortcomings of ReLU(dying ReLU problem) and LeakyReLU(inconsistent predictions for negative input values). So the authors of the paper behind PReLU thought why not let the a in ax for x<0 (in LeakyReLU) get learned!!

And here is the catch: if all the channels share the same a that gets learned, it is called channel-shared PReLU. But if each channel learn their own a, it is called channel-wise PReLU.

So what if ReLU or LeakyReLU was better for that problem? That is upto the model to learn:

1. if a is/are learned as 0 --> PReLU becomes ReLu
2. if a is/are learned as small number --> PReLU becomes LeakyReLU

Answer 3

Leaky ReLU(Leaky Rectified Linear Unit):

• is improved ReLU, being able to mitigate Dying ReLU Problem.
• can convert an input value(x) to the output value between ax and x. *Memos:
  • If x < 0, then ax while if 0 <= x, then x.
  • a is 0.01 by default basically.
• is also called LReLU.
• is LeakyReLU() in PyTorch.
• is used in:
  • GAN.
• 's pros:
  • It mitigates Vanishing Gradient Problem.
  • It mitigates Dying ReLU Problem. *0 is still produced for the input value 0 so Dying ReLU Problem is not completely avoided.
• 's cons:
  • It's non-differentiable at x=0.
• 's graph in Desmos:

PReLU(Parametric Rectified Linear Unit):

• is improved Leaky ReLU, having the 0 or more learnable parameters which are changing(adjusting) during training to improve a model's accuracy and convergence.
• can convert an input value(x) to the output value between ax and x: *Memos:
  • If x < 0, then ax while if 0 <= x, then x.
  • a is 0.25 by default basically. *a is the initial value for 0 or more learnable parameters.
• is PReLU() in PyTorch.
• is used in:
  • SRGAN(Super-Resolution Generative Adversarial Network). *SRGAN is a type of GAN(Generative Adversarial Network).
• 's pros:
  • It mitigates Vanishing Gradient Problem.
  • It mitigates Dying ReLU Problem. *0 is still produced for the input value 0 so Dying ReLU Problem is not completely avoided.
• 's cons:
  • It's non-differentiable at x = 0. *The gradient for step function doesn't exist at x = 0 during Backpropagation which does differential to calculate and get a gradient.
• 's graph in Desmos: