Micro Average vs Macro average Performance in a Multiclass classification setting

Question

I am trying out a multiclass classification setting with 3 classes. The class distribution is skewed with most of the data falling in 1 of the 3 classes. (class labels being 1,2,3, with 67.28% of the data falling in class label 1, 11.99% data in class 2, and remaining in class 3)

I am training a multiclass classifier on this dataset and I am getting the following performance:

                    Precision           Recall           F1-Score
Micro Average       0.731               0.731            0.731
Macro Average       0.679               0.529            0.565

I am not sure why all Micro average performances are equal and also Macro average performances are low compared to Micro average.

score 498 · Answer 1 · answered Oct 25 '17 at 02:33

Micro- and macro-averages (for whatever metric) will compute slightly different things, and thus their interpretation differs. A macro-average will compute the metric independently for each class and then take the average (hence treating all classes equally), whereas a micro-average will aggregate the contributions of all classes to compute the average metric. In a multi-class classification setup, micro-average is preferable if you suspect there might be class imbalance (i.e you may have many more examples of one class than of other classes).

To illustrate why, take for example precision $Pr=\frac{TP}{(TP+FP)}$. Let's imagine you have a One-vs-All (there is only one correct class output per example) multi-class classification system with four classes and the following numbers when tested:

Class A: 1 TP and 1 FP
Class B: 10 TP and 90 FP
Class C: 1 TP and 1 FP
Class D: 1 TP and 1 FP

You can see easily that $Pr_A = Pr_C = Pr_D = 0.5$, whereas $Pr_B=0.1$.

A macro-average will then compute: $Pr=\frac{0.5+0.1+0.5+0.5}{4}=0.4$
A micro-average will compute: $Pr=\frac{1+10+1+1}{2+100+2+2}=0.123$

These are quite different values for precision. Intuitively, in the macro-average the "good" precision (0.5) of classes A, C and D is contributing to maintain a "decent" overall precision (0.4). While this is technically true (across classes, the average precision is 0.4), it is a bit misleading, since a large number of examples are not properly classified. These examples predominantly correspond to class B, so they only contribute 1/4 towards the average in spite of constituting 94.3% of your test data. The micro-average will adequately capture this class imbalance, and bring the overall precision average down to 0.123 (more in line with the precision of the dominating class B (0.1)).

For computational reasons, it may sometimes be more convenient to compute class averages and then macro-average them. If class imbalance is known to be an issue, there are several ways around it. One is to report not only the macro-average, but also its standard deviation (for 3 or more classes). Another is to compute a weighted macro-average, in which each class contribution to the average is weighted by the relative number of examples available for it. In the above scenario, we obtain:

$Pr_{macro-mean}={0.25·0.5+0.25·0.1+0.25·0.5+0.25·0.5}=0.4$ $Pr_{macro-stdev}=0.173$

$Pr_{macro-weighted}={0.0189·0.5+0.943·0.1+0.0189·0.5+0.0189·0.5}={0.009+0.094+0.009+0.009}=0.123$

The large standard deviation (0.173) already tells us that the 0.4 average does not stem from a uniform precision among classes, but it might be just easier to compute the weighted macro-average, which in essence is another way of computing the micro-average.

score 47 · Answer 2 · edited Jan 06 '21 at 21:25

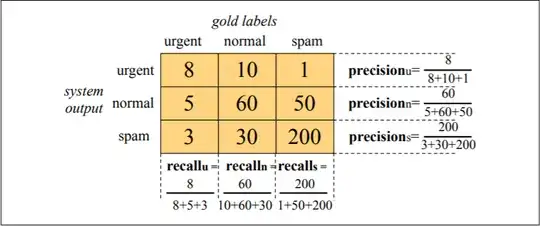
This is the Original Post.

In Micro-average method, you sum up the individual true positives, false positives, and false negatives of the system for different sets and the apply them to get the statistics.

Tricky, but I found this very interesting. There are two methods by which you can get such average statistic of information retrieval and classification.

1. Micro-average Method

In Micro-average method, you sum up the individual true positives, false positives, and false negatives of the system for different sets and the apply them to get the statistics. For example, for a set of data, the system's

True positive (TP1)  = 12
False positive (FP1) = 9
False negative (FN1) = 3

Then precision (P1) and recall (R1) will be $57.14 \%=\frac {TP1}{TP1+FP1}$ and $80\%=\frac {TP1}{TP1+FN1}$

and for a different set of data, the system's

True positive (TP2)  = 50
False positive (FP2) = 23
False negative (FN2) = 9

Then precision (P2) and recall (R2) will be 68.49 and 84.75

Now, the average precision and recall of the system using the Micro-average method is

$\text{Micro-average of precision} = \frac{TP1+TP2}{TP1+TP2+FP1+FP2} = \frac{12+50}{12+50+9+23} = 65.96$

$\text{Micro-average of recall} = \frac{TP1+TP2}{TP1+TP2+FN1+FN2} = \frac{12+50}{12+50+3+9} = 83.78$

The Micro-average F-Score will be simply the harmonic mean of these two figures.

2. Macro-average Method

The method is straight forward. Just take the average of the precision and recall of the system on different sets. For example, the macro-average precision and recall of the system for the given example is

$\text{Macro-average precision} = \frac{P1+P2}{2} = \frac{57.14+68.49}{2} = 62.82$ $\text{Macro-average recall} = \frac{R1+R2}{2} = \frac{80+84.75}{2} = 82.25$

The Macro-average F-Score will be simply the harmonic mean of these two figures.

Suitability Macro-average method can be used when you want to know how the system performs overall across the sets of data. You should not come up with any specific decision with this average.

On the other hand, micro-average can be a useful measure when your dataset varies in size.

score 28 · Answer 3 · edited Mar 14 '18 at 03:17

In a multi-class setting micro-averaged precision and recall are always the same.

$$ P = \frac{\sum_c TP_c}{\sum_c TP_c + \sum_c FP_c}\\ R = \frac{\sum_c TP_c}{\sum_c TP_c + \sum_c FN_c} $$ where c is the class label.

Since in a multi-class setting you count all false instances it turns out that $$ \sum_c FP_c = \sum_c FN_c $$

Hence P = R. In other words, every single False Prediction will be a False Positive for a class, and every Single Negative will be a False Negative for a class. If you treat a binary classification case as a bi-class classification and compute the micro-averaged precision and recall they will be same.

The answer given by Rahul is in the case of averaging binary precision and recall from multiple dataset. In which case the micro-averaged precision and recall are different.

Lerner Zhang · Answer 4 · 2021-08-17T15:32:31.810

Assume that we are classifying an email into one of the three groups: urgent, normal and spam. We compare the predicts with the ground truth labels, then we get the following confusion matrix and the recall and precision for each class.

But how can we derive a single metric that tells us how well the system is doing? There are two methods to combie these values:

In macroaveraging, we compute the performance for each class, and then average over classes. In microaveraging, we collect the decisions for all classes into a single confusion matrix, and then compute precision and recall from that table. The above figure shows the confusion matrix for each class separately, and shows the computation of microaveraged and macroaveraged precision.

What are the advantages and disadvantages of the two methods?

As the figure shows, a microaverage is dominated by the more frequent class (in this case spam), since the counts are pooled. The macroaverage better reflects the statistics of the smaller classes, and so is more appropriate when performance on all the classes is equally important.

In your case, since 67.28% of the data fall in class label 1, I guess that class label 1 dominates the microaverage and the performance of that class is better than other classes. If all classes are equally important the macroaverage is fairer.

Reference： Speech and Language Processing

score 6 · Answer 5 · answered Oct 19 '18 at 20:20

That's how it should be. I had the same result for my research. It seemed weird at first. But precision and recall should be the same while micro-averaging the result of multi-class single-label classifier. This is because if you consider a misclassification c1=c2 (where c1 and c2 are 2 different classes), the misclassification is a false positive (fp) with respect to c2 and false negative (fn) with respect to c1. If you sum the fn and fp for all classes, you get the same number because you are counting each misclassification as fp with respect to one class and fn with respect to another class.

score 4 · Answer 6 · answered Apr 02 '22 at 09:28

Multiclass Averaging

Introduction

I refer you to the original article for more details.

Sklearn documentation defines the average briefly:

'macro' : Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.

'micro' : Calculate metrics globally by counting the total true positives, false negatives and false positives.

Macro averaging

Macro averaging reduces your multiclass predictions down to multiple sets of binary predictions, calculates the corresponding metric for each of the binary cases, and then averages the results together. As an example, consider precision for the binary case. $P =\dfrac{TP}{TP+FP}$

In the multiclass case, macro averaging reduces the problem to multiple one-vs-all comparisons. The precision is calculated for each “relevant” column. This process is repeated for the other levels. The results are then averaged together.

The formula representation looks like this. For k classes:

$ P_{macro} = \dfrac{P_a + P_b + ... + P_n}{k}$

Note that in macro averaging, all classes get equal weight when contributing their portion of the precision value to the total. This might not be a realistic calculation when you have a large amount of class imbalance. In that case, a weighted macro average might make more sense

Micro averaging

Micro averaging treats the entire set of data as an aggregate result, and calculates 1 metric rather than k metrics that get averaged together.

For precision, this works by calculating all of the true positive results for each class and using that as the numerator, and then calculating all of the true positive and false positive results for each class, and using that as the denominator.

The formula representation looks like this. For k classes:

$ P_{micro} = \dfrac{TP_a + TP_b + ... + TP_n}{\left(TP_a + TP_b + ... + TP_n\right) + ( FP_a + FP_b + ... + FP_n)}$

In this case, rather than each class having equal weight, each observation gets equal weight. This gives the classes with the most observations more power.

score 3 · Answer 7 · edited Feb 06 '21 at 21:12

The advantage of using the Macro F1 Score is that it gives equal weight to all data points.

For example: Let's think of it as the F1 micro takes the Sum of all the Recall and Presession of different labels independently, so when we have class imbalance like:

T1 = 90% , T2 = 80% , T3=5

then F1 Micro gives equal weight to all the class and is not affected by the deviations in the distribution of the class log the Log loss it penalizes small deviations in the class.

goyuiitv · Answer 8 · 2019-10-11T12:24:40.257

I think the reason why macro average is lower than micro average is well explained by pythiest's answer (dominating class has better predictions and so the micro average increase).

But the fact that micro average is equal for Precision, Recall and F1 score is because micro averaging these metrics results in overall Accuracy (as micro avg considers all classes as positive). Note that if Precision and Recall are equal then F1 score is just equal to precision/recall.

As for the question if the "weighted macro-average" always going to equal the "micro average"? I did some experiments with different no. of classes and different class imbalance and it turns out that this is not necessary true.

These statements are made with assumption that we are considering all the classes of same dataset (in contrast to Rahul Reddy Vemireddy's answer)