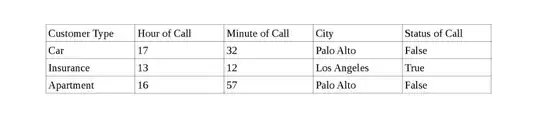
I have a dataset including a set of customers in different cities of California, time of calling for each customer, and the status of call (True if customer answers the call and False if customer does not answer).
I have to find an appropriate time of calling for future customers such that the probability of answering the call is high. So, what is the best strategy for this problem? Should I consider it as a classification problem which the hours (0,1,2,... 23) are the classes? Or should I consider it as a regression task which the time is a continuous variable? How can I make sure that the probability of answering the call will be high?
Any help would be appreciated. It also would be great if you refer me to similar problems.
Below is a snapshot of the data.