Given a 3-rank tensor with dimensions $x,y,z$.
Where:
- $x$: number of graphs (number of samples)
- $y$: number of nodes/vectors/features (let's say $5$: $a, b, c, d,$ and $e$)
- $z$: embedding dimension (e.g. $2$ for Cartesian space that consists of horizontal axis and vertical axis)
Assume that a node represents a vector. The problem is to find the relationship between the nodes whether directed (dependent), undirected (interdependent/bidirectional), or unconnected (independent).
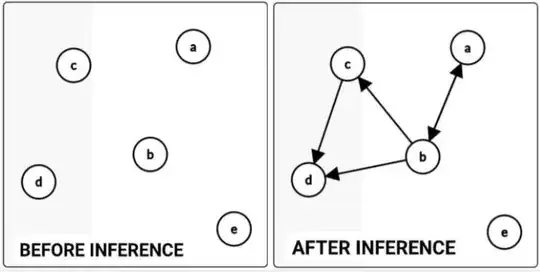
So, initially you are given unconnected nodes for all graph samples. How can you find the insight that the nodes are connected or not in a whole graph based on all samples of graphs?
This dataset can be reproduced with Random Number Generator (RNGs).
Let generate random dummy vector values for 100 samples in 2D vector:
a := RNG(dims=(100,2))
b := RNG(dims=(100,2))
c := RNG(dims=(100,2))
d := # initial d value doesn't matter
e := RNG(dims=(100,2))
Let generate dummy relationships between nodes, let's say like simple element-wise addition/multiplication or whatever as long as the operation involving dependencies of another node for un/directed relationships while no other nodes must be involved for unconnected nodes.
- $a ← a + b + 1$
- $b ← b × a + 2$
- $c ← c + b × 3$
- $d ← c^{b} + 4$
- $e ← e + 5$
That's why initial $d$ doesn't matter because there is no self dependent in its assignment.
And here is in general:
- $ a ← A(b) $
- $ b ← B(a) $
- $ c ← C(b) $
- $ d ← D(b,c) $
- $ e ← E() $
The problems are finding how many and what parameters are needed for each function $A, B, C, D$, and $E$.
In this case, the model inference is resulting:
- Function $A$ needs one parameter, node $b$.
- Function $B$ needs one parameter, node $a$, therefore $a$ and $b$ is having undirected relationship.
- Function $C$ needs one parameter, node $b$. (directed relationship).
- Function $D$ needs two parameters, node $b$ and node $c$.
- Function $E$ does not need parameters so it's safely to be said as unconnected node.
So, to summary. If I have a 3-rank tensor like $G_{x,y,z}$ and a blackbox model $F$. Performing $F(G_{x,y,z})$ will resulting insights like above, where the number of insights is depending on the number of vectors which is $y$ dimension that has length $5$.
What is the $F$? Is it a neural network? If so, how it defined?
Technically, the output of $F$ must be continuous probabilistic with the range of $[0,1]$ for each node's edge to represent dependency strongness. E.g.:
a: {b:0.8, c:0.3, d:0.2, e:0.1}
b: {a:0.9, c:0.1, d:0.2, e:0.1}
c: {a:0.1, b:0.9, d:0.1, e:0.0}
d: {a:0.1, b:0.9, c:0.8, e:0.1}
e: {a:0.1, b:0.0, c:0.0, e:0.0}
Or in table:
| From / To | a | b | c | d | e |
|---|---|---|---|---|---|
| a | - | 0.8 | 0.3 | 0.2 | 0.1 |
| b | 0.9 | - | 0.1 | 0.2 | 0.1 |
| c | 0.1 | 0.9 | - | 0.1 | 0.0 |
| d | 0.1 | 0.9 | 0.8 | - | 0.1 |
| e | 0.1 | 0.0 | 0.0 | 0.0 | - |
It's easy to solved it with neural network if there is ground truth. Where the ground truth is adjacency matrix. But, unfortunately no ground truth.