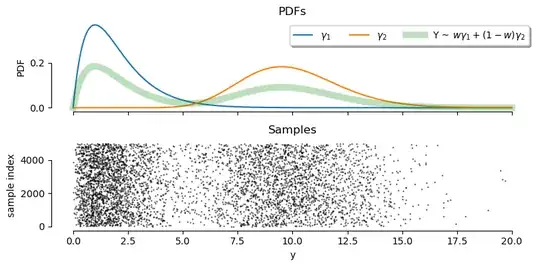
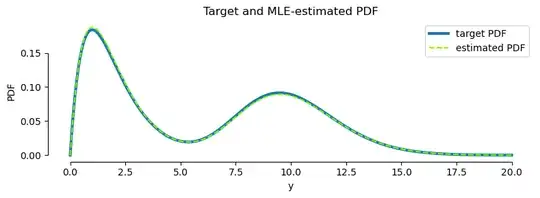
This post is just a code implementation and demo of the MLE approach outlined in this answer (generalised to multiple components using this implementation by @Galen), and the empirical CDF (ECDF) fitting approach described in the answer by @wjktrs.
I encapsulate the functionality in a GammaMixture class (originally defined by @Galen). The class provides methods for running three types of fitting for mixture parameter estimation:
Maximum likelihood estimation
- Minimizes the negative log-likelihood between the data and the mixture PDF
ECDF fitting using regular least-squares
- Minimises the MSE between the mixture CDF and the data CDF (latter estimated using a histogram)
ECDF fitting using isotonic regression
- As above, but constraining the fitted CDF to be non-decreasing (as a valid CDF should be).
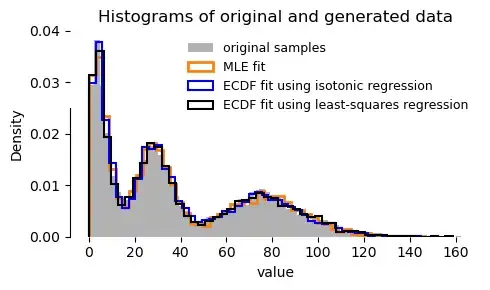
I found that the MLE approach was bar far the most stable. The ECDF fitting approaches were okay up to 3 components, but convergence was less predictable for 4+ components (the least-squares variant sometimes handled 4 components, whereas isotonic regression did not).
A comparison of fits using the three methods (sample data comprises 3 $\Gamma$ components):
Fitted CDFs:
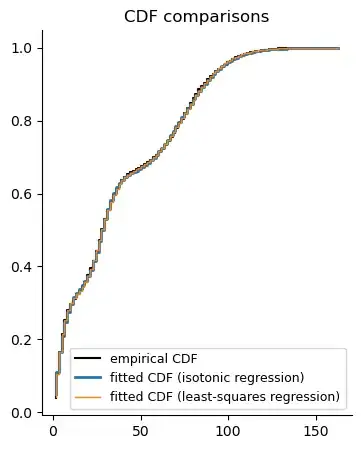
Reproducible example
Class for fitting and sampling a mixture of $\Gamma$ distributions (you can easily modify it to use other distributions defined in SciPy):
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
from scipy.special import softmax
from scipy.optimize import minimize
from typing import Tuple, Dict
class GammaMixture:
def init(self, n_components: int):
self.n_components = n_components
self.weights = np.ones(n_components) / n_components
self.alphas = np.ones(n_components)
self.scales = np.ones(n_components)
self._cdf = self._cdf_exact #alternatively: self._cdf_approx
def _pdf(self, x: np.ndarray) -> np.ndarray:
mixture = np.row_stack([
self.weights[i] * gamma.pdf(x, self.alphas[i], scale=self.scales[i])
for i in range(self.n_components)
]).sum(axis=0)
return mixture
def _cdf_approx(self, x: np.ndarray) -> np.ndarray:
"""CDF by normalising pre-computed PDF. Fast but approximate."""
pdf = self._pdf(x)
return np.cumsum(pdf / pdf.sum())
def _cdf_exact(self, x: np.ndarray) -> np.ndarray:
"""CDF exact values using SciPy"""
mixture_cdf = np.row_stack([
self.weights[i] * gamma.cdf(x, self.alphas[i], scale=self.scales[i])
for i in range(self.n_components)
]).sum(axis=0)
return mixture_cdf
def _get_initial_guesses_and_bounds(self) -> Dict[str, np.ndarray]:
initial_params = np.concatenate([
np.log(self.weights),
np.ones(2 * self.n_components) + np.random.uniform(0, 0.01, 2*self.n_components) #break symmetry
])
bounds = [(None, None)]*self.n_components + [(0, None)] * (2*self.n_components)
return {'x0': initial_params, 'bounds': bounds}
def _set_weights_alphas_scales(self, params: np.ndarray) -> None:
#Write mininmizer's results['x'] into self's weights, alphas, and scales
logits, self.alphas, self.scales = np.split(params, [self.n_components, 2*self.n_components])
self.weights = softmax(logits)
def _cdf_mse(self, params: np.ndarray, data: np.ndarray, n_bins: int) -> float:
#Compute data's ECDF. Could alternatively precompute once in calling function.
hist, bin_edges = np.histogram(data, bins=n_bins)
empirical_cdf = np.cumsum(hist / hist.sum())
#Candidate CDF
self._set_weights_alphas_scales(params)
candidate_cdf = self._cdf(bin_edges[1:])
cdf_sse = ((candidate_cdf - empirical_cdf)**2).sum()
return cdf_sse
def fit_using_ecdf(self, data: np.ndarray, n_bins: int = 100, enforce_monotonicity: bool = False) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
def _constraints_fun(params):
self._set_weights_alphas_scales(params)
_, bin_edges = np.histogram(data, bins=n_bins)
cdf = self._cdf(bin_edges)
return np.diff(cdf)
result = minimize(
fun=self._cdf_mse,
args=(data, n_bins),
**self._get_initial_guesses_and_bounds(),
constraints={'type': 'ineq', 'fun': _constraints_fun} if enforce_monotonicity else (),
)
print(
'Success?', result['success'],
'\n CDF MSE:', result['fun'],
'\n NLL: ', self._negative_log_likelihood(result['x'], data),
'\n nit: ', result['nit'],
end='\n\n'
)
self._set_weights_alphas_scales(result['x'])
return self.weights, self.alphas, self.scales
def _negative_log_likelihood(self, params: np.ndarray, data: np.ndarray) -> float:
self._set_weights_alphas_scales(params)
eps = 1e-8
neg_log_likelihood = -np.log(self._pdf(data) + eps).mean()
return neg_log_likelihood
def fit_using_mle(self, data: np.ndarray) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
result = minimize(
fun=self._negative_log_likelihood,
args=(data,),
**self._get_initial_guesses_and_bounds(),
)
print(
'Success?', result['success'],
'\n NLL:', result['fun'],
'\n nit:', result['nit'],
end='\n\n'
)
self._set_weights_alphas_scales(result['x'])
return self.weights, self.alphas, self.scales
def sample(self, n_samples: int) -> np.ndarray:
components = np.random.choice(self.n_components, size=n_samples, p=self.weights)
samples = np.array([gamma.rvs(self.alphas[i], scale=self.scales[i]) for i in components])
return samples
Compare the various fitting methods:
# np.random.seed(10)
n_per_component = 2_000
data = np.concatenate([
gamma.rvs(a=2.0, scale=3, size=n_per_component),
gamma.rvs(a=15.0, scale=2., size=n_per_component),
gamma.rvs(a=20.0, scale=4., size=n_per_component),
# gamma.rvs(a=55.0, scale=3., size=n_per_component),
])
n_components = 3
MLE fit
gamma_mixture = GammaMixture(n_components)
gamma_mixture.fit_using_mle(data)
samples_mle = gamma_mixture.sample(n_samples=len(data))
ECDF fits
gamma_mixture = GammaMixture(n_components)
gamma_mixture.fit_using_ecdf(data, n_bins=100, enforce_monotonicity=True)
samples_ecdf_isotonic = gamma_mixture.sample(n_samples=len(data))
gamma_mixture = GammaMixture(n_components)
gamma_mixture.fit_using_ecdf(data, n_bins=100, enforce_monotonicity=False)
samples_ecdf_mse = gamma_mixture.sample(n_samples=len(data))
Visualise results
f, ax = plt.subplots(figsize=(5, 3), layout='tight')
Histogram of original data
ax.hist(
data, bins=70, density=True,
color='black', alpha=0.3, label='original samples'
)
Histogram of new samples from MLE fit
ax.hist(
samples_mle, bins=50, density=True, histtype='step',
color='tab:orange', linewidth=2, label='MLE fit'
)
Histogram of new samples from CDF fit
ax.hist(
samples_ecdf_isotonic, bins=50, density=True, histtype='step',
color='blue', linewidth=1.5, label='ECDF fit using isotonic regression'
)
ax.hist(
samples_ecdf_mse, bins=50, density=True, histtype='step',
color='black', linewidth=1.5, label='ECDF fit using least-squares regression'
)
#Formatting
ax.set(xlabel='value', ylabel='Density', title='Histograms of original and generated data')
ax.legend(fontsize=9, framealpha=0)
ax.spines[['top', 'right', 'bottom']].set_visible(False)
ax.spines.left.set_bounds(0, 0.025)
For ECDF fitting methods, compare the fitted CDFs:
counts, bin_edges = np.histogram(data, bins=100, density=True)
empirical_cdf = np.cumsum(counts / counts.sum())
plt.step(bin_edges[1:], empirical_cdf, color='black', label='empirical CDF')
gamma_mixture = GammaMixture(n_components)
gamma_mixture.fit_using_ecdf(data, n_bins=100, enforce_monotonicity=True)
fitted_cdf = gamma_mixture._cdf(bin_edges[1:])
plt.step(bin_edges[1:], fitted_cdf, linewidth=2, label='fitted CDF (isotonic regression)')
gamma_mixture = GammaMixture(n_components)
gamma_mixture.fit_using_ecdf(data, n_bins=100, enforce_monotonicity=False)
fitted_cdf = gamma_mixture._cdf(bin_edges[1:])
plt.step(bin_edges[1:], fitted_cdf, linewidth=1, label='fitted CDF (least-squares regression)')
plt.title('CDF comparisons')
plt.legend(fontsize=9)
plt.gcf().set_size_inches(4, 5)
plt.gca().spines[['right', 'top']].set_visible(False)