Cross-attention mask in Transformers

Question

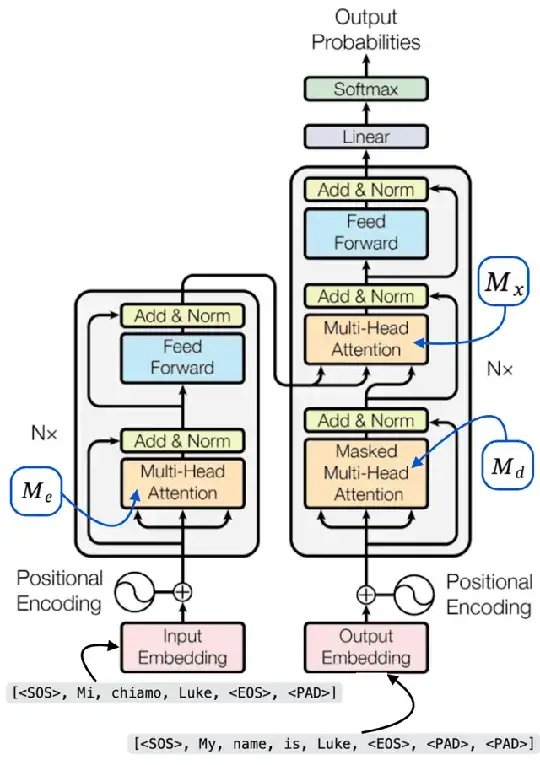
I can't fully understand how we should create the mask for the decoder's cross-attention mask in the original Transformer model from Attention Is All You Need. Here is my attempt at finding a solution: Suppose we are training such Transformer model, and we are using different-length batches for the encoder and decoder, e.g. we are trying to train an Italian-to-English machine translation model and we have:

1. The following input tokens for the Encoder:

   [<SOS>, Mi, chiamo, Luke, <EOS>, <PAD>]

   $n_e=6$ (length of encoder's input)

2. The following input tokens for the Decoder:

   [<SOS>, My, name, is, Luke, <EOS>, <PAD>, <PAD>]

   $n_d=8$ (length of decoder's input)

We have three attentions masks:

1. $M_e \in \mathbb{R}^{n_e\times n_e}$, Encoder's self attention mask.
2. $M_d \in \mathbb{R}^{n_d\times n_d}$, Decoder's self attention mask.
3. $M_x \in \mathbb{R}^{n_d\times n_e}$, Decoder's cross-attention.

Note that for the cross-attention block, given a certain embedding dimension $d_m$, we have that $Q\in\mathbb{R}^{n_d \times d_m}$, $K\in\mathbb{R}^{n_e \times d_m}$, $\frac{QK^T}{\sqrt{n_e}}\in\mathbb{R}^{n_d \times n_e} \to M_x \in \mathbb{R}^{n_d \times n_e}$

1. $M_e$ definition:

   In this case we just have to apply the padding mask to the encoder's input

   mask = [       <SOS>     Mi Chiamo   Luke  <EOS>  <PAD>  
   <SOS>        [     0,     0,     0,     0,     0,  -inf],
   Mi           [     0,     0,     0,     0,     0,  -inf],
   Chiamo       [     0,     0,     0,     0,     0,  -inf],
   Luke         [     0,     0,     0,     0,     0,  -inf],
   <EOS>        [     0,     0,     0,     0,     0,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,  -inf]
   ]
   

   We zero-out all the elements belonging to the columns that correspond to the token, this way we are sure that the embeddings for the <PAD> token won't contribute to the computation of the new values $V^{'}=\sigma(\frac{QK^T}{\sqrt{n_e}} + M_e)V$. (Where $\sigma$ is the softmax function)

2. $M_d$ definition:

   In this case it should be enough to define the causal mask to the decoder's input

   mask = [       <SOS>     My   Name     is   Luke  <EOS>  <PAD   <PAD>  
   <SOS>        [     0,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf],
   My           [     0,     0,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf],
   Name         [     0,     0,     0,  -inf,  -inf,  -inf,  -inf,  -inf],
   is           [     0,     0,     0,     0,  -inf,  -inf,  -inf,  -inf],
   Luke         [     0,     0,     0,     0,     0,  -inf,  -inf,  -inf],
   <EOS>        [     0,     0,     0,     0,     0,     0,  -inf,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,     0,     0,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,     0,     0,     0]
   ]
   

   We don't care about the padding mask because through the causal mask we implicitly ignore the values corresponding to the <PAD> tokens.

3. $M_x$ definition: I don't understand if we should combine the causal mask with the padding mask from the encoder output

   mask = [       <SOS>     Mi Chiamo   Luke  <EOS>  <PAD>  
   <SOS>        [     0,  -inf,  -inf,  -inf,  -inf,  -inf],
   My           [     0,     0,  -inf,  -inf,  -inf,  -inf],
   Name         [     0,     0,     0,  -inf,  -inf,  -inf],
   is           [     0,     0,     0,     0,  -inf,  -inf],
   Luke         [     0,     0,     0,     0,     0,  -inf],
   <EOS>        [     0,     0,     0,     0,     0,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,  -inf]
   ]  
   

   or if we should just apply the padding mask (since the VALUES are coming from the encoder, and we should have full access over the whole encoder's input)

   mask = [       <SOS>     Mi Chiamo   Luke  <EOS>  <PAD>  
   <SOS>        [     0,     0,     0,     0,     0,  -inf],
   My           [     0,     0,     0,     0,     0,  -inf],
   Name         [     0,     0,     0,     0,     0,  -inf],
   is           [     0,     0,     0,     0,     0,  -inf],
   Luke         [     0,     0,     0,     0,     0,  -inf],
   <EOS>        [     0,     0,     0,     0,     0,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,  -inf],
   <PAD>        [     0,     0,     0,     0,     0,  -inf]
   ]  
   

   Is this the right way to implement the different attention masks? What's the right alternative for the cross-attention values and what's the rational behind it? Any valid and useful resource is welcome. Thank you!

EDIT: The rational behind the latter alternative, that personally makes a little more sense to me, is depicted here:

$ \text{Legend}\to \color{orange}{\text{Decoder}} ,\ \color{green}{\text{Encoder}} \\ \color{orange}{Q^{'}}=\sigma(\frac{\color{orange}{Q}\color{green}{K}^T}{\sqrt{n_e}} + M_x)\color{green}{V} = \\ \sigma\left(\color{orange}{ \tiny \begin{bmatrix} Q_{\text{<SOS>}_0} & Q_{\text{<SOS>}_1} & \dots & Q_{\text{<SOS>}_{d_m}} \\ Q_{\text{My}_0} & Q_{\text{My}_1} & \dots & Q_{\text{My}_{d_m}} \\ Q_{\text{Name}_0} & Q_{\text{Name}_1} & \dots & Q_{\text{Name}_{d_m}} \\ Q_{\text{Is}_0} & Q_{\text{Is}_1} & \dots & Q_{\text{Is}_{d_m}} \\ Q_{\text{Luke}_0} & Q_{\text{Luke}_1} & \dots & Q_{\text{Luke}_{d_m}} \\ Q_{\text{<EOS>}_0} & Q_{\text{<EOS>}_1} & \dots & Q_{\text{<EOS>}_{d_m}} \\ Q_{\text{<PAD>}_0} & Q_{\text{<PAD>}_1} & \dots & Q_{\text{<PAD>}_{d_m}} \\ Q_{\text{<PAD>}_0} & Q_{\text{<PAD>}_1} & \dots & Q_{\text{<PAD>}_{d_m}} \end{bmatrix} } \color{green}{ \tiny \begin{bmatrix} K_{\text{<SOS>}_0} & K_{\text{Mi}_0} & K_{\text{Chiamo}_0} & K_{\text{Luke}_0} & K_{\text{<EOS>}_0} & K_{\text{<PAD>}_0} \\ K_{\text{<SOS>}_1} & K_{\text{Mi}_1} & K_{\text{Chiamo}_1} & K_{\text{Luke}_1} & K_{\text{<EOS>}_1} & K_{\text{<PAD>}_1} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ K_{\text{<SOS>}_{d_m}} & K_{\text{Mi}_{d_m}} & K_{\text{Chiamo}_{d_m}} & K_{\text{Luke}_{d_m}} & K_{\text{<EOS>}_{d_m}} & K_{\text{<PAD>}_{d_m}} \end{bmatrix} }\cdot\frac{1}{\sqrt{n_e}} + M_x\right)\color{green}{V} = $ $ \sigma\left( { \tiny \begin{bmatrix} \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{My}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{My}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{My}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{My}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{My}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{My}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{Name}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{Is}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{Luke}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<PAD>}} \\ \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<EOS>}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<PAD>}} \end{bmatrix}}\cdot\frac{1}{\sqrt{n_e}} + M_x \right)\tiny{ \color{green}{ \begin{bmatrix} V_{\text{<SOS>}_0} & V_{\text{<SOS>}_1} & \dots & V_{\text{<SOS>}_{d_m}} \\ V_{\text{Mi}_0} & V_{\text{Mi}_1} & \dots & V_{\text{Mi}_{d_m}} \\ V_{\text{Chiamo}_0} & V_{\text{Chiamo}_1} & \dots & V_{\text{Chiamo}_{d_m}} \\ V_{\text{Luke}_0} & V_{\text{Luke}_1} & \dots & V_{\text{Luke}_{d_m}} \\ V_{\text{<EOS>}_0} & V_{\text{<EOS>}_1} & \dots & V_{\text{<EOS>}_{d_m}} \\ V_{\text{<PAD>}_0} & V_{\text{<PAD>}_1} & \dots & V_{\text{<PAD>}_{d_m}} \end{bmatrix}} }= \color{orange}{ \tiny \begin{bmatrix} Q^{'}_{\text{<SOS>}_0} & Q^{'}_{\text{<SOS>}_1} & \dots & Q^{'}_{\text{<SOS>}_{d_m}} \\ Q^{'}_{\text{My}_0} & Q^{'}_{\text{My}_1} & \dots & Q^{'}_{\text{My}_{d_m}} \\ Q^{'}_{\text{Name}_0} & Q^{'}_{\text{Name}_1} & \dots & Q^{'}_{\text{Name}_{d_m}} \\ Q^{'}_{\text{Is}_0} & Q^{'}_{\text{Is}_1} & \dots & Q^{'}_{\text{Is}_{d_m}} \\ Q^{'}_{\text{Luke}_0} & Q^{'}_{\text{Luke}_1} & \dots & Q^{'}_{\text{Luke}_{d_m}} \\ Q^{'}_{\text{<EOS>}_0} & Q^{'}_{\text{<EOS>}_1} & \dots & Q^{'}_{\text{<EOS>}_{d_m}} \\ Q^{'}_{\text{<PAD>}_0} & Q^{'}_{\text{<PAD>}_1} & \dots & Q^{'}_{\text{<PAD>}_{d_m}} \\ Q^{'}_{\text{<PAD>}_0} & Q^{'}_{\text{<PAD>}_1} & \dots & Q^{'}_{\text{<PAD>}_{d_m}} \end{bmatrix} } $

Our constraint on the newly obtained $\color{orange}{Q^{'}}$ values is expressed below:

$ \color{orange}{ \tiny \begin{bmatrix} Q^{'}_{\text{<SOS>}_0} & Q^{'}_{\text{<SOS>}_1} & \dots & Q^{'}_{\text{<SOS>}_{d_m}}\\ Q^{'}_{\text{My}_0} & Q^{'}_{\text{My}_1} & \dots & Q^{'}_{\text{My}_{d_m}} \\ Q^{'}_{\text{Name}_0} & Q^{'}_{\text{Name}_1} & \dots & Q^{'}_{\text{Name}_{d_m}} \\ Q^{'}_{\text{Is}_0} & Q^{'}_{\text{Is}_1} & \dots & Q^{'}_{\text{Is}_{d_m}} \\ Q^{'}_{\text{Luke}_0} & Q^{'}_{\text{Luke}_1} & \dots & Q^{'}_{\text{Luke}_{d_m}} \\ Q^{'}_{\text{<EOS>}_0} & Q^{'}_{\text{<EOS>}_1} & \dots & Q^{'}_{\text{<EOS>}_{d_m}} \\ Q^{'}_{\text{<PAD>}_0} & Q^{'}_{\text{<PAD>}_1} & \dots & Q^{'}_{\text{<PAD>}_{d_m}} \\ Q^{'}_{\text{<PAD>}_0} & Q^{'}_{\text{<PAD>}_1} & \dots & Q^{'}_{\text{<PAD>}_{d_m}} \end{bmatrix} } \color{black}{ \tiny \begin{matrix} \to\text{Should only contain information from }\color{orange}{Q_\text{<SOS>}} \color{white}{,\text{My}} \color{white}{\text{Name,}} \color{white}{\text{Is,}} \color{white}{\text{Luke,}}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}}\ \ \ \ \ \ \ \ \ \ \ \\ \to\text{Should only contain information from }\color{orange}{Q_{\text{<SOS>}}}, \color{orange}{Q_\text{My}} \color{white}{\text{Name,,}} \color{white}{\text{Is,}} \color{white}{\text{Luke,}}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}}\ \ \ \ \ \ \ \\ \to\text{Should only contain information from }\color{orange}{Q_{\text{<SOS>}}}, \color{orange}{Q_{\text{My}}}, \color{orange}{Q_\text{Name}} \color{white}{\text{Is,,}} \color{white}{\text{Luke,}}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}}\ \ \ \ \ \ \\ \to\text{Should only contain information from }\color{orange}{Q_{\text{<SOS>}}}, \color{orange}{Q_{\text{My}}}, \color{orange}{Q_{\text{Name}}}, \color{orange}{Q_\text{Is}} \color{white}{\text{Luke,}}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}}\ \ \ \ \\ \to\text{Should only contain information from }\color{orange}{Q_{\text{<SOS>}}}, \color{orange}{Q_{\text{My}}}, \color{orange}{Q_{\text{Name}}}, \color{orange}{Q_{\text{Is}}}, \color{orange}{Q_\text{Luke}}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}}\ \ \\ \to\text{Should only contain information from }\color{orange}{Q_{\text{<SOS>}}}, \color{orange}{Q_{\text{My}}}, \color{orange}{Q_{\text{Name}}}, \color{orange}{Q_{\text{Is}}}, \color{orange}{Q_{\text{Luke}}}, \color{orange}{Q_{\text{<EOS>}}}\ \ \\ \to\text{We don't care}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}}\\ \to\text{We don't care}\color{white}{Q^{'}_{\text{<PAD>}_{d_m}}} \end{matrix} } $

And I see no reason to define a causal mask given that each row in $\color{orange}{Q}\color{green}{K}^T$ contains information about the corresponding token in the decoder (i.e. the first row contains information about the first token $\color{orange}{\text{<SOS>}}$, the second row contains information about the second token $\color{orange}{\text{My}}$, and so on...)

$ { \tiny \begin{bmatrix} \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<SOS>}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{<SOS>}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{My}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{My}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{My}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{My}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{My}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{My}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{Name}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{Name}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{Name}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{Is}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{Is}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{Is}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{Luke}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{Luke}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{Luke}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<EOS>}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{<EOS>}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{<PAD>}}\cdot\color{grey}{\text{<PAD>}} \\ \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<SOS>}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Mi}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Chiamo}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{Luke}} & \color{orange}{\text{<PAD>}}\cdot\color{green}{\text{<EOS>}} & \color{grey}{\text{<PAD>}}\cdot\color{grey}{\text{<PAD>}} \end{bmatrix}} $

Answer 1

I don't understand if we should combine the causal mask with the padding mask from the encoder output or if we should just apply the padding mask (since the VALUES are coming from the encoder, and we should have full access over the whole encoder's input)

For a translation scenario, here are what the masks should be:

• Encoder mask: don't attend to <PAD> or irrelevant tokens. Typically, the encoder can have access to the full sequence.

An edge case where you would mask out future tokens could be: You need to simulate a scenario where your input comes in a streaming fashion and make a prediction before knowing if the stream ends.

• Decoder mask: don't attend to tokens that "don't exist" yet. In practice, when you decode, you typically do it one token at a time, so you don't know yet about the future tokens.

But that's only for cases where your decoder aims to generate a next token. Let's say you have a textual entailment task where you need to provide the relationship between input A and B. If you model your task as a next token generation (i.e. entailment/no entailment), you might want to give your decoder full context over the input as it would act as "another" encoder

• Cross-attention mask: Similarly to the previous two, it should mask input that the model "shouldn't have access to". So for a translation scenario, it would typically have access to the entire input and the output generated so far. So, it should be a combination of the causal and padding mask.

Well-written question, by the way.

Answer 2

From the paper:

"We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions. This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position i can depend only on the known outputs at positions less than i."

which means that the causal mask is applied exclusively to the self-attention layer.

This is evident from PyTorch's official Transformer implementation

# From TransformerDecoderLayer's forward() pass:
# ...
# Self-Attention
x = self.norm1(x + self._sa_block(x, tgt_mask, tgt_key_padding_mask, tgt_is_causal))
# Cross-attention (note: tgt mask is not passed)
x = self.norm2(x + self._mha_block(x, memory, memory_mask, memory_key_padding_mask, memory_is_causal))
x = self.norm3(x + self._ff_block(x))
# memory: encoder's output
# ...
...