Multiple Hypothesis Testing in feature selection process

Question

I am doing feature selection of features which are of binary nature i.e. each feature represents presence or absence of a substructure in a molecule. And I have a target variable of two classes. My first step was to check if my feature is associated with the target variable so I was using chi-square test for that.And later I check if the selected features have any correlation and remove that. So each feature is checked for association with target variable using chi square test. I am wondering if any correction methods are needed here in my case like bonferroni or false discovery rate. If yes what are the assumptions I should keep in mind. Really appreciate the help.

Answer 1

In a basic statistical model like a logistic regression on the features, this kind of univariate feature selection is problematic. Briefly, a candidate feature can be fairly unrelated to the outcome on its own but become quite important once another feature is considered. If you do univariate screening, you miss out on that kind of important feature.

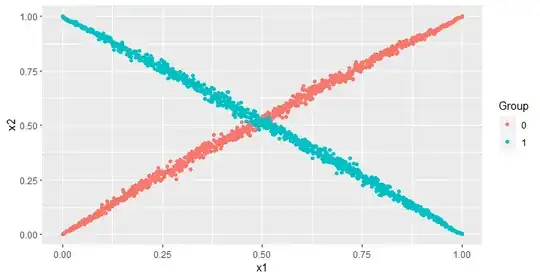
If you use a more sophisticated machine learning model like a random forest or a neural network, even a logistic regression with feature interactions, then univariate screening is even more problematic. Consider the image below (taken from another post of mine).

Jointly, the two features almost perfectly distinguish between red and blue. However, neither feature, alone, is at all correlated with the color. If you have interaction terms in a logistic regression or run a model like a random forest or neural network that will interact features as it sees fit, then you miss out on these being important features, even if their importance only happens in the interaction.

You can explicitly test for a correlation between the interaction and the outcome, which would reveal the interaction in this case to be extremely important, but then you're doing univariate screening (the interaction feature is, after all, a candidate feature), which is problematic as described above.

(I consider a chi-squared test to be a correlation-style measure, due to the relationship between chi-squared testing and a score test in a logistic regression, so I am content to use a bit of slang when I write "correlation".)