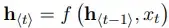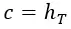I was trying to read RNN Encoder Decoder paper.
RNN (plain RNN i.e. non encoder-decoder RNN)
It starts with giving equation for RNN:
hidden state in RNN is given as:
... equation (1)where f is a non linear activation function.
The output is a softmax:
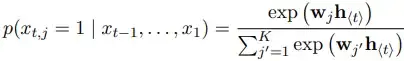... equation(2)
for all possible symbols j = 1, ..., K.
RNN encoder-decoder
Then it explains RNN encoder-decoder:
- The RNN encoder decoder architecture is given as follows:
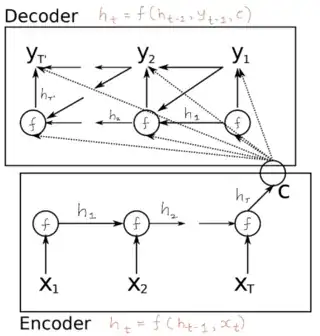
- There are two equations for encoder:
- The encoder hidden state equation is same as that for plain RNN, i.e. equation (1)
- The summary of the whole input sequence, which is indicated by letter c is nothing but the hidden state produced after reading last input word. (c for "context" as that forms input context for decoder):
- The decoder hidden state is calculated as follows:
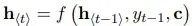
This is indicated by circles in decoder in above image each of which takes y_(t-1), c and h_(t-1) as input.
What I am not able to get is how y_t is calculated in decoder? Is it by using softmax as in equation(2). If yes exactly how? Note that diagram shows three inputs for calculating y_t: h_t, c and y_(t-1). How these inputs are incorporated for calculating y. The paper does not seem to discuss this, or am I misreading?
Update
I just found that paper says:
for an activation function g which must produce valid probabilities, e.g. a softmax. But still its unclear how exactly these three (h_t, y_(t-1) and c) variables can be included in softmax.
