Artificial Neural Networks and Efficient Parameter Optimization

Question

I have a bunch of test measurements data and a semi-empirical model that has 18 parameters which I have to find so that the model fits my data well. So far I've managed to find and optimise the parameters using Optimisation and Global Optimisation algorithms in MATLAB.

Now I would like to explore different approaches for the parameter estimation. I have read some papers where the approach with NNs is described. I am new to NNs and have no idea if this is even possible.

I would create a two layer network with 18 input and output neurons. I am not sure what kind of transfer function would be appropriate for the problem.

The formula I have to fit and find the parameters look like this:

$ y = D \sin(C \arctan(Bx - E(Bx - \arctan(Bx))))$

where $B, C, D, E$ are macro-coefficients and the micro-coefficients are used to express the variation of each of the primary coefficients with respect to some other data.

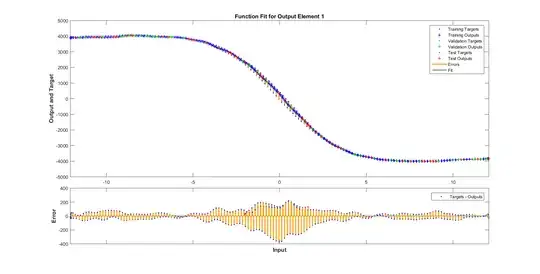
This is how my data looks like. How would you create network in MATLAB for this problem? Can you give me some hints and a push in the right direction to tackle this problem?

Thanks in advance.

Answer 1

If you were fitting a large number of different models, and you had sequences of training data for each different model (with the params already known in those cases), then you might be able to use a recursive neural network (RNN) to provide param estimates for new data sequences. However, that does not seem to be your situation.

As I understand your question, you have a mathematical model with some free parameters, and one set of data that you would like to use to estimate those parameters.

A neural network is not really of any use to you here. That is because the neural network would replace your semi-empirical model with the NN, and the free parameters become the weights of the NN. The trained NN would not match your desired model, but would generically fit to the data. It could be used to predict more function outputs given the inputs - the NN might even do better than your preferred model, which would be an interesting result implying that your model is incomplete.

Often we don't know (or perhaps even care) about an underlying parsimonious model. In this case, ML techniques that fit params of a generic model to data using some objective function like squared error can be very useful tools. However, when we do have a good idea about a simple or explanatory model, those same techniques are less useful, and instead we can use optimisers direct on the model - in some cases these could be the same optimisers used to train neural networks, provided the model is differentiable.