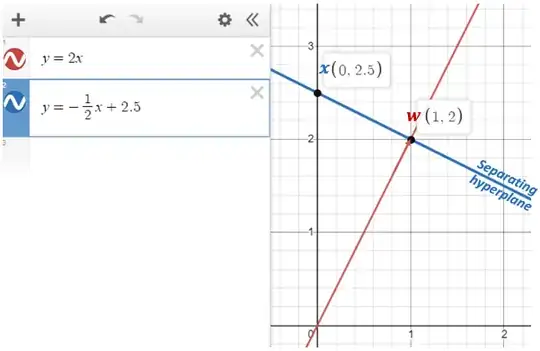
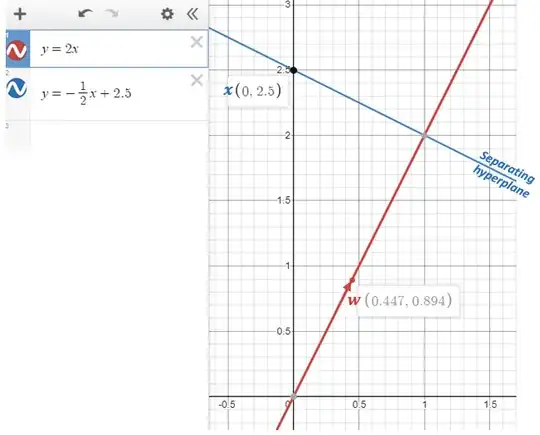
I was wondering if I can visualize with the example the fact that for all points $x$ on the separating hyperplane, the following equation holds true:
$$w^T.x+w_0=0\quad\quad\quad \text{... equation (1)}$$
Here, $w$ is a weight vector and $w_0$ is a bias term (perpendicular distance of the separating hyperplane from the origin) defining separating hyperplane. I was trying to visualize in 2D space. In 2D, the separating hyperplane is nothing but the decision boundary. So, I took following example: $w=[1\quad 2], w_0=\Vert w\Vert=\sqrt{1^2+2^2}=\sqrt{5}$ and $x=[0\quad 2.5]$. (Check at the bottom of the post, how I came up with these.)
But I don't find this example make above equation true: $$\color{red}{\begin{bmatrix} 1 \\2 \end{bmatrix}\begin{bmatrix} 0 & 2.5 \end{bmatrix}-\sqrt{5}=5-\sqrt{5}\neq 0}$$
However, I then realized that making $w$ a unit vector makes equation (1) true:
$$\begin{bmatrix} 1/\sqrt{5} \\2/\sqrt{5} \end{bmatrix}\begin{bmatrix} 0 & 2.5 \end{bmatrix}-\sqrt{5}=\sqrt{5}-\sqrt{5}= 0$$
So, I have following few related questions:
Q1. Does equation (1) applies "only to" unit weight vector? (In read some texts which scale this equation to make $w$ a unit vector) Is there any way to make equation (1) work for non-unit weight vector?
Q2. Are weight vectors always considered to be unit vectors? (that is even during actual implementation, do they turn out to be unit vector?)
How I come up with the graph
First, assumed $w=[1\quad 2]$. The slope of the vector will be $2$. So to plot line passing through the vector and origin, I plotted $y=2x$. The slope of the line perpendicular to this line will be negative inverse of slope of this line, that is it will be $-1/2$. So to plot a line (separating plane or decision boundary) perpendicular to $y=2x$ and not passing through the origin, but through $y=2.5$, I plotted a line $y=-\frac{1}{2}x+2.5$.