Any finite Graph G with all V have at least degree of 2, is it true that every vertex is necessarily contained IN a cycle?

Question

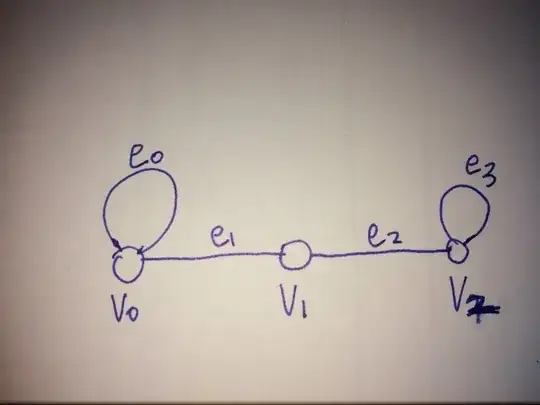
As title, (note: this questions is asking weather or not all vertices are contained IN a cycle not asking if the G contains a cycle.

My attempt is that:

So this graph would be an counter example that disprove that every vertex is contained in a cycle. Would like to know if this is a valid counter-example since V1 is not contained in a cycle.

PS: As I was finding examples, also observed that if the all V have exactly degree of 2, then it is necessary that all vertices are contained in a cycle. Please prove if I am missing something.

Answer 1

You are asking two questions. The first question is whether your graph is a counterexample to the claim that in a graph with minimum degree 2, every vertex lies in a simple cycle. Unfortunately, your graph is not simple, so if by graph you mean simple undirected graph, then your graph is not a counterexample. However, if you replace the self-loop by a cycle, you should get a valid counterexample.

The second question is whether the claim is true if the graph is 2-regular (all degrees are 2). Indeed, a 2-regular graph is a disjoint union of cycles. I'll leave you to figure out a proof.