What is the best way to merge cycles to minimise total weight?

Question

Suppose I have a vertex-disjoint set $S$ of simple cycles in a weighted undirected graph. So no vertex $v$ is contained in more than one cycle. A cycle $c$ is a closed path with no repeated vertices: $c=(v_1, v_2, \ldots, v_n)$, where $v_n=v_1$. Each edge $e=(v_i,v_j)$ has a positive weight $w(e)$. The weight of a cycle $w(c)$ is the sum of its edge weights: $w(c) = w(v_1,v_2)+\ldots+w(v_{n-1},v_n)$. The total weight of $S$ is the sum of all its cycle weights.

Naively I want to merge all the cycles in $S$ into a single cycle with the smallest total weight. I also want to somehow preserve most of the edges of the original cycles. I am not looking for an optimal solution, just an efficient heuristic.

I can merge two cycles by removing an edge from each one and connecting them up with new edges. For example, suppose I have two cycles $c=(v_1, v_2, \ldots, v_n)$ and $c'=(v'_1, v'_2, \ldots, v'_k)$. I can remove edges $(v_a,v_{a+1}), (v'_b,v'_{b+1})$ and add edges $(v_a,v'_b), (v_{a+1},v'_{b+1})$ to form a single cycle $(v_1, \ldots, v_a, v'_b, \ldots, v'_{b+1}, v_{a+1}, \ldots, v_1)$. This move is somewhat similar to 2opt and there are O(nk) such moves possible. I can continue merging cycles in this fashion until I reach a single cycle. Essentially I am building a minimal spanning tree that spans cycles.

Although the above procedure works in giving me a single cycle, it rarely gives me a cycle with a small weight. I can enhance this procedure by merging 3 cycles at once in a move similar to 3opt, but then I have to perform significantly more computations.

So here are my questions:

• Is this a well known problem?
• Can I improve the efficiency of this approach?
• Is there an efficient heuristic that produces a cycle of small weight?

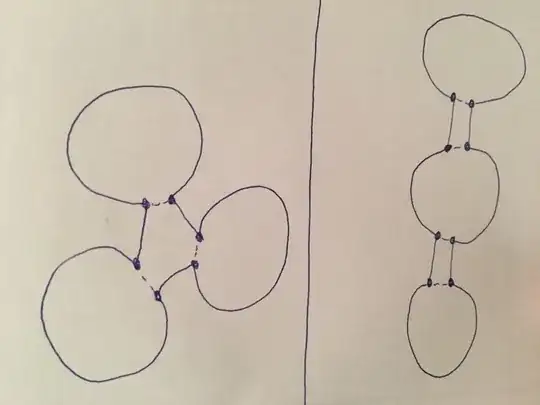
Attached are some examples. In the left figure a 3opt move is optimal, while in the right figure a sequence of 2opt moves is best.

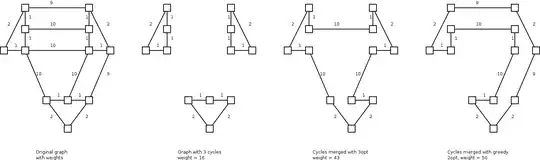
Here is a numeric example that I constructed. Using the optimal merging method we get a weight of 43, while the greedy algorithm gives us a worse solution of weight 50. Even if we join the bottom cycle by removing the new edge we added (weight 10) we would still get a worse solution (I didn't draw it for clarity).

Answer 1

If you realize that you actually looking for algorithms that generate tours from cycles, then the problem amounts guaranteeing that the generated tour will contain many of the cycles' edges.

I suggest to delete from the original graph all edges that are not cycle edges but connect a pair of vertices of the same cycle, i.e. delete every cycle's diagonals, and then run any of algorithm that calculates near optimal solutions of the TSP on the resulting graph; Christofides' algorithm, Held & Karp, double tree, tour expansion, etc. come to mind for heuristics.

Answer 2

This is NOT an answer. This post is just to construct a concrete numeric example out of the left diagram in the picture in the question.

(This answer, too long to fit as a comment, was requested by a user who wanted to see a concrete numeric example which his greedy algorithm may fail. It was written about the same time when OP added a numeric example that is exactly the same except a slightly different weight assignment.)

Let $G$ be the complete undirected graph on 12 vertices $A_1, A_2, A_3, A_4, B_1, B_2, B_3, B_4, C_1, C_2, C_3, C_4$.

Let $S$ be the set of the following three simple circles.

• the circle $c_A$: $A_1, A_2, A_3, A_4, A_1$.
• the circle $c_B$: $B_1, B_2, B_3, B_4, B_1$.
• the circle $c_C$: $C_1, C_2, C_3, C_4, C_1$.

All edges in the three circles weigh 1. The edges $A_3B_2, A_4B_1, B_3C_2, B_1C_4, C_3A_2$ and $C_4A_3$ weigh 2. - All other edges weigh 16.

We are allowed to merge two cycles by removing an edge from each cycle and connecting them up with two new edges, repeatedly until we reach a single cycle. The goal is to reach a cycle with the smallest total weight.

A description of an optimal solution for $S$.

1. Remove edge $A_2A_3$ and $B_2B_3$. Add edge $A_3B_2$ and $A_2B_3$.
2. Remove edge $A_2B_3$ and $C_2C_3$. Add edge $B_3C_2$ and $C_3A_2$.

We end up with the simple cycle $A_1, A_4, A_3, B_2, B_1, B_4, B_3, C_2, C_1, C_4, C_3, A_2, A_1$, which has weight $3* 2+ 9*1 = 15$.

A description of greedy algorithm on $S$ that considers all pairs of two existing cycles at a time.

1. Since the three cycles are symmetric, WLOG, let us merge cycle $C_a$ and cycle $C_b$. To avoid adding an edge whose weight is 16, we have only one choice. Remove edge $A_3A_4$ and $B_1B_2$. Add edge $A_3B_2$ and $A_2B_3$. The resulting circle, named $c_{AB}$, is $A_1, A_2, A_3, B_2, B_3, B_4, B_1, A_4, A_1$.
2. Now it is time to merge $c_C$ and $c_{AB}$. To avoid adding an edge whose weight is 16, we have only two choices. We can either remove $B_3B_4$ and $C_1C_2$ and add $B_3C_2$ and $B_4C_1$, resulting with cycle $A_1, A_2, A_3, B_2, B_3, C_2, C_3, C_4, C_1, B_4, B_1, A_4, A_1$, whose weight is $4 * 2 + 8 * 1 = 16$. Or we can remove $C_3C_4$ and $A_1A_2$ and add $C_3A_2$ and $C_4A_1$ cycle, resulting with cycle $C_1, C_2, C_3, A_2, A_3, B_2, B_3, B_4, B_1, A_4, A_1, C_4, C_1$, with the same weight 16.

Conclusion: A simple greedy algorithm does not guarantee the desired smallest weight.

I have also constructed a planar graph out of that left diagram. However, it is much more messier to describe the construction and to show the algorithms and their results.

Furthemore, it is not hard to construct an example where the greedy algorithm that considers all triples of existing cycles at a time will not reach the smallest weight. I believe, with a bit of more work, we can show a greedy algorithm that considers all combinations of a fix number of existing cycles does not guarantee the desired smallest weight.

It is quite possible this problem does not have a polynomial solution that always yields the smallest weight. In fact, it looks like this concern is implied by the OP since the question asks for "an efficient heuristic that produces a cycle of small weight".