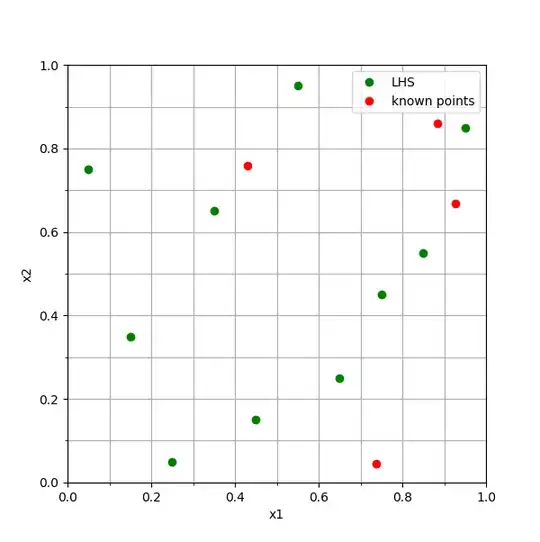
I use Latin hypercube sampling to select what point to evaluate my function. As evaluations take a lot of time, I want to limit the time by adding already evaluated points.
I thought about taking the min distance between the points, and if I have an already evaluated point that is near on LHS point, I remove the LHS to minimize the number of evaluations. Sadly this is not how LHS works, and the results are not very good.
You've divided the x values into 10 columns, and divided the y values into 10 rows, so we have a 10x10 grid.
Take any row that is already covered by some already evaluated point, and remove it from the set of rows. Do the same with the columns. In your picture, we are left with 6 rows and 6 columns. Consider the 6x6 grid obtained by looking only at those 6 rows and 6 columns.
Now use your Latin hypercube sampling strategy on a 6x6 grid, to cover each of those 6 rows and each of those 6 columns. This gives you 6 points that cover the 6x6 grid. Now this can be interpreted as 6 points in the 10x10 grid, and if you combine those 6 points with the 4 existing points, you'll see that the result covers every row and every column exactly once.
