Finding the number of squares by connected coordinates

Question

If I have a list of lists as below ,

 [[1, 2], [3, 4], [1, 5], [2, 6], [4, 8], [5, 6], [6, 7],
 [7, 8], [6, 10], [7, 11], [8, 12], [10, 11],
 [10, 14], [12, 16], [14, 15], [15, 16]] 

and

[[1, 2], [2, 3], [3, 4], [1, 5], [4, 8],
     [6, 7], [5, 9], [6, 10], [7, 11], [8, 12],
     [9, 13], [10, 11], [12, 16], [13, 14], [14, 15], [15, 16]] 

The above 2 lists can be visualized as in the image, where each point is represented by a list.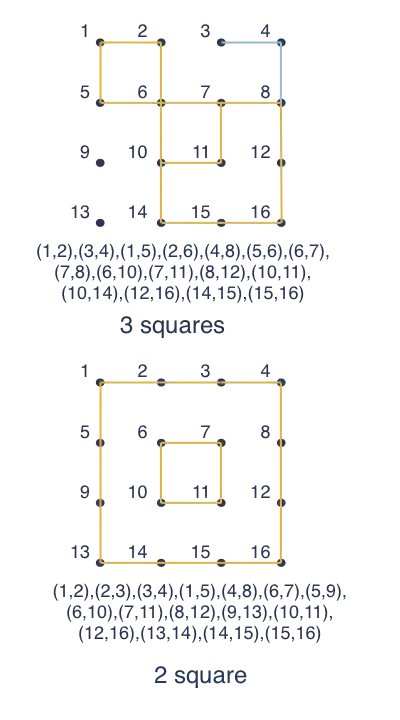

I know there is a graph traversal where every visited node can be tracked as we traverse through the graph. But in this case, there is no direction mentioned.

How should I approach this problem? I am also interested in hints.

Answer 1

Let $b(p, \ell)$ be a boolean value denoting whether the horizontal segment whose left endpoint is $p$ and whose length is $\ell$ exists. Then the values of $b(p,\ell)$ for all possible $p$ and $\ell$ can be computed in $O(n^3)$ recursively using the fact that

$b(p,\ell)$ is true iff $b(p,\ell-1)$ is true and $b(p+\ell-1,1)$ is true where $p+\ell-1$ denotes the point on the right side of $p$ and the distance between them is $\ell-1$.

Here $n$ is the length of the grid.

Similarly, you can do the same thing for vertical segments.

Now you can check each possible square by checking its four edge segments. The whole running time is $O(n^3)$.

---

As j_random_hacker said in the comment,

You can drop the space usage to $O(n^2)$ by instead calculating the length $w(p)$ of the longest horizontal segment having left endpoint $p$ for all $p$. Then $b(p,\ell)=(w(p)\ge\ell)$.

Answer 2

A square is determined by the location of its upper-left corner and the length of its sides. You can enumerate all possibilities for that and check whether the picture does indeed contain that square or not.