Regarding the median of medians solution to the $k$th smallest element in an array, why does the algorithm split the array into subarrays of length $n/5$, where $n$ is the length of the initial array? Why not $n/7$ or $n/3$? Why 5??
1 Answers
Along with the explanation given on wikipedia, I'll try to give more visual examples. The main point is that subarrays of length $ \frac{n}{3}$ make it a non-linear algorithm.
We can actually check out the 3 scenarios you discuss. I'm going to be referring to area diagrams similar to the one depicted on wikipedia. These area diagrams are a useful abstraction to see how large of a subproblem we might have to recurse on in the worst case. The area diagrams will look something like this:
Where $M$ is median of medians, $(< M)$ and $(> M)$ represent the area (amount of values in the array) that are potentially less than $M$ and greater than $M$ respectively, in the worst/best case. Note that in the area diagrams I present I say the area is roughly (~) some value. This is because it may be off by one or two and I am largely ignoring these small constants because they will be insignificant to the analysis. If you are bothered by this, you can assume $n$ is of a useful form such that the values are exact.
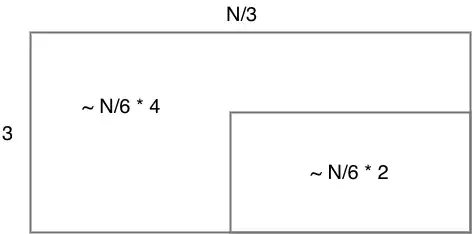
For $\frac{n}{3}$ size subarrays we will end up with an area diagram like this:
It is clear that in the worst case we will have to recurse on roughly $\frac{4 n}{6}$ elements in the array. This will give us a recurrence relation: $$\begin{align} T(n) & = T\left(\frac{n}{3}\right) + T\left(\frac{4n}{6}\right) + cn\\ & = T\left(\frac{n}{3}\right) + T\left(\frac{2n}{3}\right) + cn \end{align}$$ This actually turns out to be on the order of $O(n \log n)$. I won't go through an explicit proof of this recurrence because I'm sure it's been done before. If you wish to prove it to yourself, you can use a similar approach to this, or use the recursion tree method, or use the Akra-Bazzi method. So this subarray size won't work because we now have non-linear time complexity.
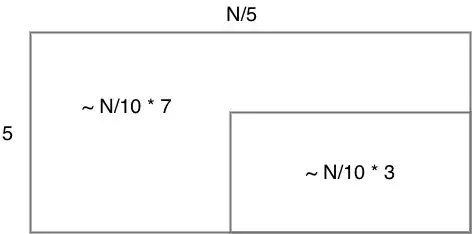
For $\frac{n}{5}$ size subarrays we will end up with an area diagram like this:
We similarly get a worst-case recurrence of the following:
$$T(n) = T\left(\frac{n}{5}\right) + T\left(\frac{7n}{10}\right) + cn$$
This is linear $O(n)$! You can use this method directly to prove it is linear.
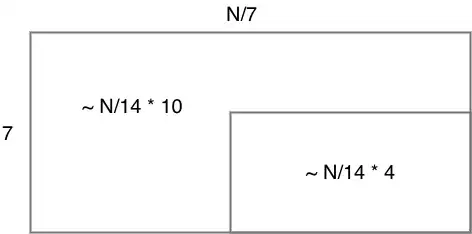
For $\frac{n}{7}$ size subarrays we will end up with an area diagram like this:
We similarly get a worst-case recurrence of the following:
$$T(n) = T\left(\frac{n}{7}\right) + T\left(\frac{10n}{14}\right) + cn$$
This is also linear! Again, you can use the method I described above to prove this.
So in conclusion
Diving the subarrays into length $\frac{n}{3}$ will not be good because it is non-linear! Diving the subarrays into length $\frac{n}{5}$ or $\frac{n}{7}$ will be very good because it is linear! You can actually go on to use $\frac{n}{9}, \frac{n}{11}, \ldots$ and still get linear time!
- 4,533
- 1
- 16
- 41