How does one easily determine if an algorithm has an exponential time complexity? The Word Break naive solution is known to have a time complexity of O(2n) but most people think its O(n!) because of the decreasing subsets as you go down the stack depth.
Word Break Problem: Given an input string and a dictionary of words, find out if the input string can be segmented into a space-separated sequence of dictionary words.
The brute-force/naive solution to this is:
def wordBreak(self, s, wordDict):
queue = [0]
dictionary_set = set(wordDict)
for left in queue:
for right in range(left,len(s)):
if s[left:right+1] in dictionary_set:
if right == len(s)-1:
return True
queue.append(right+1)
return False
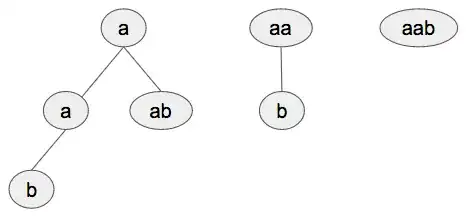
With the worst case inputs of:
s = 'aab'
wordDict = ['a','aa','aaa']
Results in a O(2n) time complexity of 23 ≈ 7:
Let me caveat this question with:
- I'm not looking for a performant solution so just ignore why the implementation is the way it is. There is a known O(n2) dynamic programming solution.
- I know there are similar questions asked on stackexchange, but none of them gave an easy to understand answer to this problem. I would like a clear answer with examples using preferably the Word Break example.
- I can definitely figure the complexity by counting every computation in the code, or using recurrence relation substitution/tree methods but what I'm aiming for in this question is how do you know when you look at this algorithm quickly that it has a O(2n) time complexity? An approximation heuristic similar to looking at nested for loops and knowing that it has a O(n2) time complexity. Is there some mathematical theory/pattern here with decreasing subsets that easily answers this?