While studying Automata at my University, I faced the following problem from SIPSER, M textbook:
Consider D = { w | w contains an even number of as and an odd number of bs and doesn't contains the chain ab}. Draw an DFA with 5 states that recognizes D and a Regular Expression that generated D.
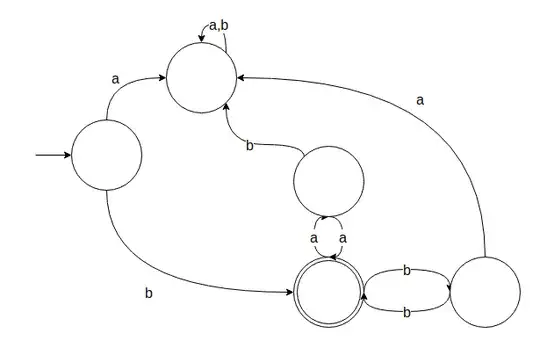
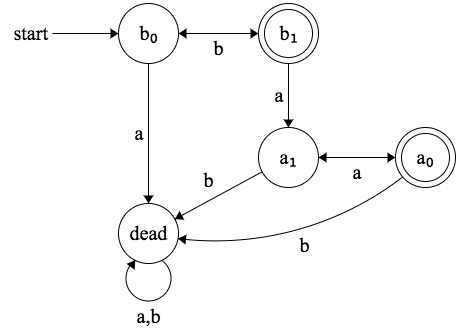
I tried doing the following DFA:
With the Regular Expression b(bb)*(aa)*
And that seemed quite right for me, but for chains that goes like baab it should be refused, but it isn't.
I couldn't find a way to fix it without adding another state to the DFA.
How can it be done?