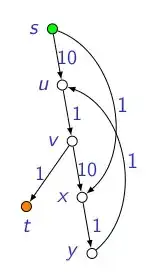
I read that shortest path using DFS is not possible on a weighted graph. I pretty much understood the reason of why we can't apply on DFS for shortest path using this example:-
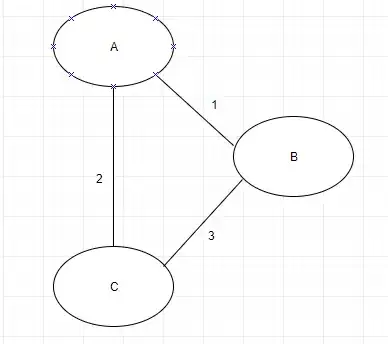
Here if we follow greedy approach then DFS can take path A-B-C and we will not get shortest path from A-C with traditional DFS algorithm.
I think that we can modify DFS slightly in this way to get shortest path.In this example, after the DFS goes through A-B-C and comes back again to A, we can check all adjacent nodes and if the distance from A to any of the adjacent node is less than the distance which was assigned previously(i.e 2<4) then we visit the node again even if the node is visited again before and continue the DFS from this node (like visiting C again). If we do this way, ofcourse the complexity will be bad but I don't think that its impossible to get shortest path using DFS. Is this the right approach?
Initially we have cost array initialized to infinity except for source vertex which is initialized to 0. dist(u,v) denotes edge weight from vertex u to vertex v.
function spath(vertex u)
{
for each(vertex v adjacent to u)
{
if(cost[u] + dist(u,v) < cost[v])
{
cost[v]=cost[u]+dist(u,v);
parent[v]=u;
spath(v);
}
}
return;
}