Traditionally, this kind of problem is described as a fractional factorial design problem. However, your problem also can be elegantly solved via a probabilistic / statistical method that exploits the power of low discrepancy sequences.
For additional context, this method can be applied to very similar questions as yours, such as:
Low Discrepancy Sequences
Low discrepancy sequences, (often described as quasirandom sequences) are numbers that generally appear random, but have an underlying structure to them that makes them more evenly distributed and so have less 'gaps' and 'clumping'.
There are many ways to construct low discrepancy sequences, and they can be generalised to arbitrarily high dimensions, too. For example, below is a picture of the first 100 terms of five different low discrepancy sequences in two dimensional and how they compare to simple random sampling. Note that all of them are substantially more evenly distributed than the conventional uniform random sampling.
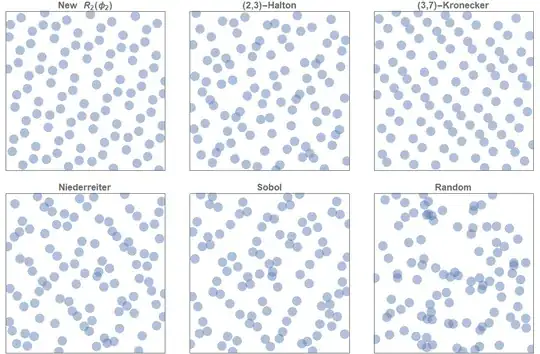
Further details can be found at the Wikipedia article: "Halton Sequence".
Equidistributed Allocation
A post I wrote, "The unreasonable effectiveness of quasirandom sequences" , describes how to easily create an efficient extensible $d$-dimensional low discrepancy sequences. (For this particular case, we need a $d=3$ dimensional sequence.)
Define an $n$ x $3$ dimensional array, where each of the $n=200$ rows represents a different trial, and each of the components of each 3-vector defines which type of variety to use for each of the $d=3$ categories.
For $d=3$, there is one magical number involved which is $ \phi_3 = 1.2207440846... $ (see the article if you are interested in what is so special about this number).
Now simply define for all integer $n$, a 3-dimensional vector $\pmb{t}_n$ such that:
$$ \mathbf{t}_n = \pmb{s} + n \pmb{\alpha} \; (\textrm{mod} \; 1), \quad n=1,2,3,... $$
$$ \textrm{where} \quad \pmb{\alpha} =(\frac{1}{\phi_3}, \frac{1}{\phi_3^2},\frac{1}{\phi_3^3}).$$
In nearly all instances, the choice of initial seed $\pmb{s} $ does not change the key characteristics, and so for reasons of obvious simplicity, $\pmb{s} =\pmb{0}$ is the usual choice. (I have included it in this definition, because if you wish to create another sampling distribution, all you need to do is re-run the code but with a different starting seed!)
Specifically for $d=3$; with $\phi_3 = 1.2207440846$ and $\pmb{s}= (0.5,0.5,0.5) $, the first 5 terms of this sequence are:
- (0.319173, 0.171044, 0.0497005)
- (0.138345, 0.842087, 0.599401)
- (0.957518, 0.513131, 0.149101)
- (0.77669, 0.184174, 0.698802)
- (0.595863, 0.855218, 0.248502)
...
Now consider the first component $x_n$ of each vector $t_n$, to represent the first category ("Maize"). (ie $x_1 = 0.319173$). If
- $ 0 \leq x < 1/7$, then select Maize, option A
- $ 1/7 \leq x < 2/7$, then select Maize, option B
- $ 2/7 \leq x < 3/7$, then select Maize, option C
- ...
- $ 6/7 \leq x < 1$, then select Maize, option G
Similarly, consider the second component $y_n$ of each vector $t_n$, to represent the second category ("Fertilizer"). If
- $ 0 \leq x < 1/4$, then select Fertilizer, option A
- $ 1/4 \leq x < 2/4$, then select Fertilizer, option B
- $ 2/4 \leq x < 3/4$, then select Fertilizer, option C
- $ 3/4 \leq x < 1$, then select Fertilizer, option G
Summary
The beautiful result of this low discrepancy method is that, for any $n$, the number of varieties allocated in each category will not differ by more than 1.
Said another way, the number of samples for every variety and every category, will never be more than 1 away to the ideal equal allocation method.
Code
Python code to create the low discrepancy sequences is
# Use Newton-Rhapson-Method
def gamma(d):
x=1.0000
for i in range(20):
x = x-(pow(x,d+1)-x-1)/((d+1)*pow(x,d)-1)
return x
d=3
n=200
g = gamma(d)
alpha = np.zeros(d)
s=0.5 # initial seed.
for j in range(d):
alpha[j] = pow(1/g,j+1) %1
z = np.zeros((n, d))
for i in range(n):
z = (s + alpha*(i+1)) %1
print(s)
print(z)
Hope that helps!
