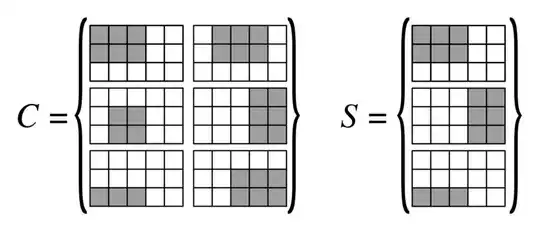
Thanks to j_random_hacker's hint, I've found a solution to reduce Vertex Cover to the Grid Problem:
We make a $|E|$-by-$|V|$ grid of 3-by-3 blocks, i.e. a $3|E|$-by-$3|V|$ grid, with vertices ordered as columns $\{v_1,\dots,v_{N_1}\}$ and edges ordered as rows $\{e_1,\dots,e_{N_2}\}$.
We'll construct rectangles on this grid (the drawing below will help a lot understanding the different rectangles used)
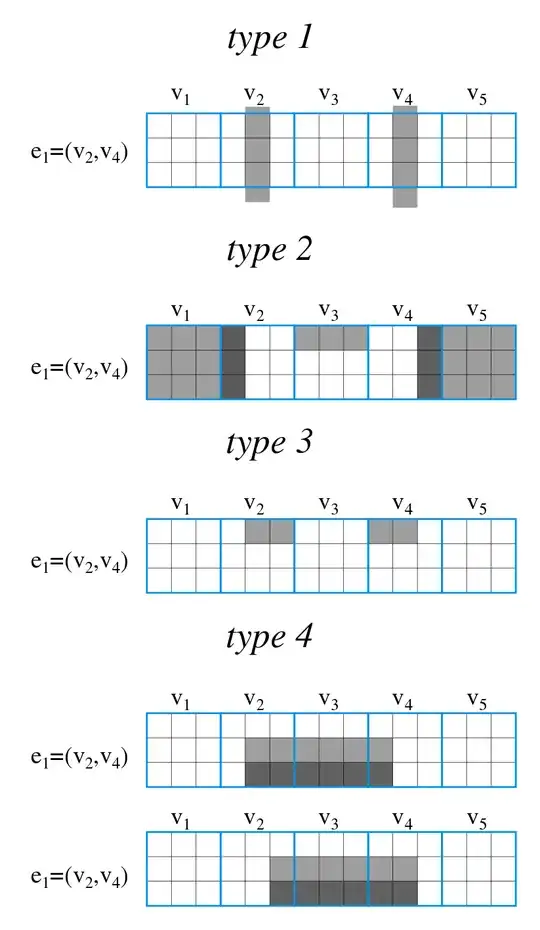
For each vertex, we create a rectangle of type 1, which covers the central column of the column of blocks corresponding to that vertex, so we have $|V|$ rectangles of type 1.
Each block correspond to a unique couple $(e_i,v_j)$, with $e_i=(v_a,v_b)$ for each block we add a rectangle of type 2 :
- if $j<a$ or $b<j$, this is a 3-by-3 rectangle covering the entire block.
- if $j=a$ (resp. $j=b$), this is a 3-by-1 rectangle covering of the left (resp. right) column of the block.
- if $a<j<b$, this is a 1-by-3 rectangle covering the top row of the block.
So we have $|E||V|$ rectangles of type 2, those rectangles will be obligatory to choose, as each will be the only cover for the top-left (or top-right) corner of the block it's in.
As we have said, each edge correspond to a row, with two blocks (let's call them endblocks) corresponding to the endpoints of the vertices $(e_i,v_a)$ and $(e_i,v_b)$, now we have rectangles of type 3:
- for endblock $(e_i,v_a)$ (resp. $(e_i,v_b)$), we have a 1-by-2 rectangle covering the top-right (resp. top-left) corner of the endblock.
We have $2|E|$ rectangles of type 3, and again, they're obligatory as each will be the only cover for the top-right corner (if it's the first endblock) or the top-left corner (if it's the second endblock) it's in.
Now, for each edge we construct rectangles of type 4, between the endblocks, we have two rectangles for the second row :
- One going from the central square of the first block to the central-left square of the second block.
- One going from the central-right square of the first block to the central square of the second block.
- And the same two rectangles for the third row.
We have $4|E|$ rectangles of type 4, those are not all obligatory however.
So now, to cover the grid:
- $|E|(|V|+2)$ rectangles (type 2 and 3) are obligatory and $|V|+4|E|$ (type 1 and 4) are optionnal.
To cover, for a given edge, the part between the edge endblocks not yet covered (second and third rows of the row of blocks), we can either use:
- the four rectangle of type 4.
- one rectangle of type 1 and two rectangles of type 4.
Note that in any case, we need at least two rectangles of type 4.
So here the cost function will be : $|E|(|V|+4) + k$
If their is a valid vertex cover with less than k vertex: we use the $|E|(|V|+2)$ obligatory rectangles, then for the optionnal rectangles, we can use the rectangles of type 1 corresponding of the vertex cover, and for every row, we need only 2 rectangles of type 4 (we already have a rectangle of type 1). So if the graph has a valid vertex cover, the grid has a valid set cover.
If we have a valid set cover for the grid (with less than $|E|(|V|+4) + k$) rectangles, then for each edge, either we already have a rectangle of type 1 (and the edge is "covered") or four rectangle of type 4, in which case, we can replace two of them by one rectangle of type 1, and we still have a valid cover with $|E|(|V|+4) + k$ rectangles. By iterating this process, we reach a valid solution with no row using four rectangle of type 4, from which we can obtain a valid vertex cover.
So the vertex cover can be reduced to the grid cover. And the grid problem instance can be encoded by $|E|(|V|+6) + |V|$ covers on a grid with $9|V||E|$ elements, so the reduction is polynomial and the grid problem is NPC.
PS :
I noticed after writing this answer that a lot of rectangles are actually useless and much simpler reduction can be made using a $|E|$-by-$3|V|$ grid with $|V|+4|E|$ covers, using cost function $3|E|+k$