reduction from SET-COVER to VERTEX-COVER

Question

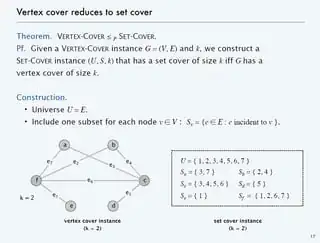
I've come with an idea for reduction from the set-cover problem to the vertex-cover problem, But I'm not sure if this reduction is correct. I saw in this post's comments that "There cannot be a nice reduction of this sort".

Consider the set of $S$ to be $S_1,...,S_n$ where the element of $S$ is $s_1, ..., s_m$. In the graph $G=(V,E)$ for each $S_i$ there is a vertex, and an edge from $S_i$ to $S_j$ will be iff there is some element $x\in S_i \land x\in S_j$.

is this reduction even right?

score 5 · Accepted Answer · edited Mar 09 '22 at 03:51

5

No, since $\{\{0,1\},\{1\}\}$ and $\{\{0,1\},\{1,2\}\}$ yield isomorphic graphs.

But the sizes of their minimum set covers are different.

edited Mar 09 '22 at 03:51

upe

161
8

answered Jun 01 '17 at 09:58

score 1 · Answer 2 · 2018-01-30T20:04:41.877

Another reason which may help understanding why this reduction (from Set Cover to Vertex Cover) is not possible is as follows. See the slide below (taken from Kleinberg, Tardos).

Here, a single element (represented as an edge) appears in exactly two sets (nodes). If this was not the case (and an element appeared in less than or more than two sets), drawing such a graph would not be possible (an edge can only have exactly two ends (nodes)).

Going from Vertex Cover to Set Cover is easy because Vertex Cover is applied on a graph that already exists (we do not need to draw a graph).

Edit (by Discrete lizard): Constructing such a graph from arbitrary sets is possible, but then there must be multiple edges representing the same element. The construction of a graph fails for another reason: there may be at most one edge for every pair of nodes, which need not be the case for arbitrary sets.

score 0 · Answer 3 · edited Jan 24 '21 at 09:25

A special case of set cover problem is able to do this reduction.

Let 2SC be the Set Cover problem restricted to instances where each item appears in at most two sets.

Given instance $\langle U,S={S_1,S_2,\ldots}\rangle$, reduction from 2SC to vertex cover: create an edge for each elements in U where each edge in $S_i$ share a common endpoint $v_i$. Then, U is transformed to the universal set of edges, $S_i$ is the adjacent neighbors of $v_i$. Pick $S_i$ in 2SC is equivalent to pick $v_i$ in vertex cover.

Actually, 2SC and VC are equivalent.

reduction from SET-COVER to VERTEX-COVER

3 Answers3