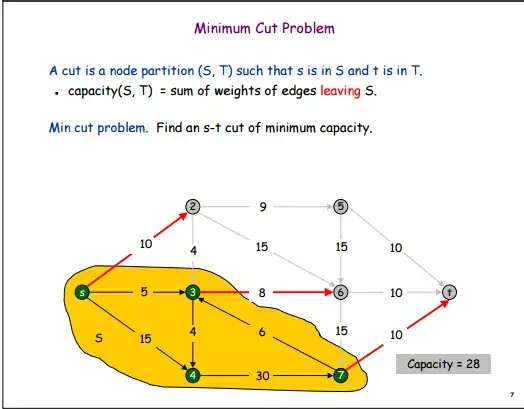
I was reading about max flow theorem and there I saw scenario where the min s-t cut is found. But wherever I searched they did it after knowing the max flow or by guessing the cuts by iterating almost all .
Is there a logical way to arrive at the minimum cut (with the paths) without knowing the maximum flow or guessing the cuts ?
Added thought: In a graph of say N vertices, and say one is source 's' and other is sink 't'. So there are 2^(N-2) possible s-t groupings. This is huge even for N = 8. So is iterating all the only way to get the answer. I was told that it is being asked in exams. Is it fair to ask such an itertative procedure in exam of limited time. How can one be sure that he has arrived at the correct answer without checking all (or without being given the max flow value)? For eg. finding the min cut as explained here .