Adjacency matrix and recognizing hierarchy?

Question

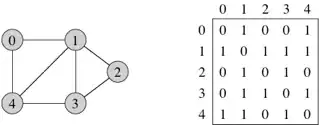
I'm currently learning about graphs and I have some questions regarding adjacency matrices. Given an arbitrary adjacency matrix:

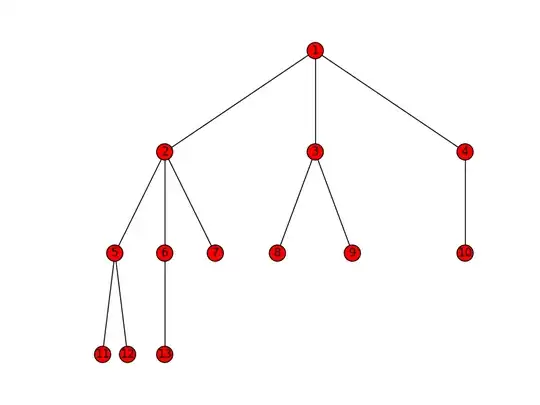
Is there any way to tell if that matrix represents a hierarchal graph structure? Obviously in the above case it's not.

Something like:

I know the rows of and i x i adjacency matrix represent the out-degree of ith vertex and columns represent the in-degree of the ith vertex. But is there any way to tell just by looking at the general structure of the adjacency matrix if the graph is hierarchical (At least, for smaller matrices as above) ?

Answer 1

By definition you can check if a graph is a tree (regardless of its representation) with these facts:

1. The graph does not have cycles.
2. It only has a single connected component.

The first condition can be checked with a simple DFS checking if there is a back edge. The connected components can be counted using either DFS or BFS.

Regarding to an adjacency matrix, every tree is a bipartite graph. See this, but keep in mind that proving that a a graph is bipartite does not mean it is a tree.