The intervals are represented as two numbers, e.g. $(4.3, 5.6)$. The intervals are unique.
If for $(x,y)$ and $(u,v)$, $x≤u$ and $v≤y$, $(u,v)$ is nested in $(x,y)$
How do I find out which intervals are nested in others efficiently?
The hint is to use two induction hypotheses: one to assume you can solve the problem for $n-1$ intervals, another that you can find the largest right endpoint for the $n-1$ intervals.
How do I use this information to do the inductive step in constant time?
This problem is as hard as comparison sorting, given n input number sort them.
You can make interval set from input number set $S$ (w.l.o.g suppose input numbers are in $Z^+$) as follow:
$ \Gamma = \{(a,b) \mid a\in S \wedge b=\max_{t\in S} \{2\cdot t - a + 1 \} \}$
Above transformation can be done in $O(n)$.
But if you find a nesting relation in this interval set in $o(n \log n)$, you can sort input array in $o(n \log n)$, But comparison sorting barrier is $\Omega(n \log n)$, So the algorithm which finds interval nesting cannot be better than $\Omega(n \log n)$ with respect to comparision sorting barrier, But also $O(n \log n)$ algorithm is trivial.
A solution must look like this: we have list of intervals and we must tell for a new interval which of the intervals contain it and which of the list are contained in the new interval.
A logical start will be that the list of intervals are sorted in some data structure and we need to add the new interval in its proper place. In the general case an insertion into some sorted list can be done in time complexity $O(log n)$, when using self-balancing binary search tree for example.
I am not sure if for the general case it is possible to reach $O(1)$ time. However to beat the logarithmic time you may need to add some limitations. It is clear that for the insertion we must not use comparison. One limited solution can be done by using modified counting sort. This however will work only if we know that the interval's points are limited to positive integer values in some interval(you can enhance the solution to work for sets that are countable and finite, if you assume that you don't have infinite memory).
Example: If we have $n=4$ the following list $(1, 8), (3, 6), (2, 3)$ and you want to add a new interval $(4, 5)$
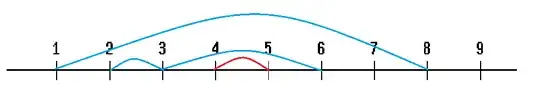We can order them in array with size $n$ X largest right endpoint: in the first row we place interval's IDs in the cell with the number of the start/end point. If this cell already has an ID we are using the cell in the bottom row. We can keep a counter to the fullness level of each column.
We can add the same way the new interval in $O(1)$ time and have the intervals ordered by their nesting again in constant time.
Here is some pseudo code of the operaion in the n-th step:
Input:new_interval = (x,y)
array[x][x_column_counter] = new_interval_id
array[y][y_column_counter] = new_interval_id
y_column_counter++
x_column_counter++
