Steps to convert regular expressions directly to regular grammars and vice versa

Question

I came across following intuitive rules to convert basic/minimal regular expressions directly to regular grammar (RLG for Right Linear Grammars, LLG for Left Linear Grammars):

Then I came across many examples that claimed to use these rules to prepare regular grammars from given regex. However I was not able to understand how they are actually using these rules, as they directly gave final regular grammar for given regex. So I decided to try some examples step by step and find whats going on.

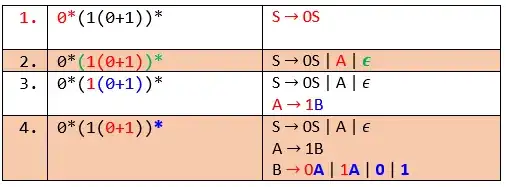
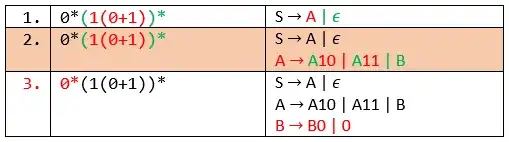
Below is one such examples which tries to step by step find RLG and LLG for regex $0^*(1(0+1))^*$. At each step, same color is used to match part of regex getting translated into corresponding part in grammar.

Preparing RLG

Notice that rule in first table says $e^*$ gets translated to RLG productions taking form $S\rightarrow eS | \epsilon$. However in example above, we can see that, to emulate * in regex, we have to put $\epsilon$ in step 2 (green color) as indicated by the rule, but also need to add bunch of other stuff in step 4 (blue color), which are not directly indicated by the rule (though somewhat intuitive extension of the rule).

Preparing LLG

While preparing LLG also, we can see that, to emulate * in regex, we have to put $\epsilon$ (green colored) in step 1 as indicated by the rule, but also need to add bunch of other stuff in step 2 (green colored), which are not directly indicated by the rule (though again somewhat intuitive extension of the rule).

Apart from star closure, there are many stuff that I dont find straight forward or at least requiring extra awareness (that cannot be easily put in step-by-step procedure) while preparing grammar. For example, while preparing RLG, to emulate $0^*$, I can do $S\rightarrow 0S|\epsilon$ as indicated by first table. But in above example, I have to remain extra aware that there is something more $((1(0+1))^*)$ after $0^*$ which forces me to put $A$ in $S\rightarrow 0S | A | \epsilon$ production in step 2. Other facts I should be aware of:

• While preparing RLG, I should start from left of the regex
• While preparing LLG, I should start from right of the regex

I observed many more such small points which all I need to be aware at each step of preparing grammar. It makes me feel fuzzy.

Am I going correct with this at all? Is there any book which discuss regex to regular grammar direct conversion, giving clear step by step procedure? Or there is simply no such procedure and I am unnecessarily trying to make it up from examples?

Answer 1

As (briefly) indicated by Raphael in a comment, the only difference between an NFA and a linear grammar is formatting. You can use any algorithm which converts a regular expression to an NFA, and produce a right or left linear grammar instead of the NFA, simply by changing the way you produce output.

Specifically, when you are producing an NFA (with any algorithm) you will perform a series of steps of the form "Add a transition labeled $a$ between $P$ and $Q$", where $a$ is either a terminal or $\varepsilon$, and $P$ and $Q$ are states. To "directly" produce a right linear grammar, implement the above step by producing the production $P\to a Q$ if $a$ is a terminal, or $P\to Q$ if $a$ is ε. Also, implement the step "Mark $Q$ as a final (accepting) state" by outputting the production $Q\to\varepsilon$. (Alternatively, don't put $Q$ in the productions produced for transitions, if you know in advance that $Q$ is a final state.)

If you want to produce a left linear grammar, you need to work with incoming transitions instead of outgoing transitions; for the $a$-transition from $P$ to $Q$, write $Q\to P a$ unless $P$ is the start state, in which case you just use $Q\to a$. (Again, ε transitions are handled by omitting $a$.)

If the unit productions bother you, use an algorithm which produce an ε-free NFA, or produce the NFA and then do an ε closure to eliminate the ε transitions before printing out the grammar.

Any correct regular expression to linear grammar algorithm will be some version of the above procedure (since you could produce the transition table instead of the grammar by once again changing the print format).