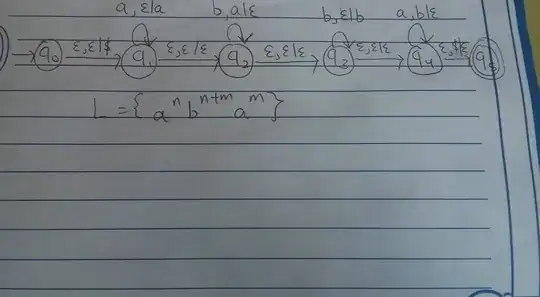0

Give a question: Language L= {a^n b^(n+m) a^m}, where both n and m are >=0. Is L context-free or not.

If the answer is yes, can I use the following PDA to prove it?

Since {a^n b^(n+m) a^m}={a^n b^n b^m a^m}, in the PDA, we first push n a's onto the stack. Then, we pop n a's from the stack by reading n b's. Next, we push m b's onto the stack, and we pop m b's from the stack by reading m a's. Finally, the strings will be accepted in q5.

enter image description here

Conversely, if the language is not context-free, should i use pumping lemma to prove it?

Thank you!

Gareth Lam
  • 3
  • 3

3 Answers3

3
S → AB  
A → aAb | ε  
B → bBa | ε

This will be the Grammar for that language which follows the context free grammar rules, so the language generated will be CFL.

Pavan Kumar Munnam
  • 398
  • 3
  • 12
1

If the answer is yes, can I use the following PDA to prove it?

Yes you can. Context-free languages are the languages generated by context-free grammars but also those accepted by push-down automata. So, if you are not explicitly asked to do so, then there is no need to rewrite your PDA into a CFG.

Also note that there exist procedures to transform a PDA into a CFG (or vice versa). This will usually not give you an elegant grammar, but a guaranteed answer. From your notation of your PDA I guess you use Sipser's book. He describes a method that ties the moment where a symbols is pushed on the stack is tied to the same symbol being popped.

Hendrik Jan
  • 31,459
  • 1
  • 54
  • 109
-3

The language as you told is a union 2 languages (one for a^nb^n and other one is a^mb^m). As cfls are closed under union even your language is regular. I did not understand your pda notation to validate it.

Vinod Pn
  • 123
  • 3