7

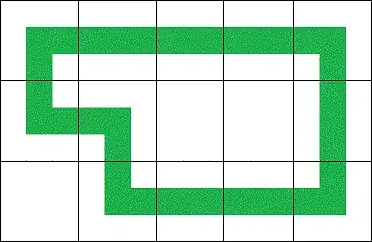
I have to build a cycle with fixed length $n$ that includes exactly $k$ corners inside $w$ x $h$ rectangle.

For example:
$w = 5\\h=3$

$n = 12\\k = 6$

Rectangle

I have already found out that I need at least $4$ corners and number of corners and number of non-corner elements needs to be even number.

Then I write an recursive algorithm that runs in exponential time complexity, but I have a strong feeling that this thing can be done much faster.

Problem is that I do not know which square will definitely be in the cycle so I run my algorithm on first $\frac w2$ fields to cover all chances, but I am aware that I search some branches multiple time.

I have also discovered that if the cycle exist it will start with corner in (0, 0) or corner in (0, 1)

Does anybody have an idea on how to speed this thing up?

Have a nice day!

Evil
  • 9,525
  • 11
  • 32
  • 53
A J
  • 83
  • 5

1 Answers1

-1

your problem looks inherently exponential to me to find all the solutions. a rough sketch to show that is to create a large # of similar-looking objects. the objects are the same under translation and rotation. they (apparently?) can also be scaled. so in a rough sense there is no way to "speed it up" if you already have an exponential time algorithm. you ask for a better algorithm but also ask for general ideas. here are some ideas/ suggestions.

  • youve abstracted the problem but it might help to step back and describe the background that inspired it. is it from some field in particular? chances are there are papers that study the general area.

  • it looks like its in NP because its easy to verify solutions. think of solving it in terms of NP. a canonical problem in this area is the satisfiability problem. many problems have been converted to it and SAT solvers are "state of the art" for solving NP problems. SAT solvers can discover and handle the intrinsic symmetries in the problem not technically "efficiently" (in the sense of guaranteed P time) but in the "most efficient way known" based on heuristics, "best practices", and decades of optimization research/ theory. so consider translating it to SAT and studying it that way.

  • if you want a general idea of the algorithm behavior you can run it at different scales and graph the # of solutions to find basic scaling properties.

  • if you just want any solution, you might try a probabilistic approach where you lay down a simple starting shape say square/ rectangle and then randomly alter it until it gets closer to your requirements. see eg heuristics. genetic algorithms are also good for this. you can encode the shape in terms of genetic coding.

  • imagine a triangular shape that has 2 straight sides at right angles and then a 3rd that is diagonal and has any # of corners required. its not an "efficient" use of space because it has a large open area but it satisfies your criteria and can be created at any scale with arbitrary # of corners. you didnt specify any criteria about minimizing or maximizing space inside or outside. so maybe this is a bit underconstrained as stated.

  • actually think this might need to be described better. are you touching squares only at the edges squares and the squares touching those edge squares? what do you mean by "corners"? corners on your object? corner squares on the rectangle? you give only one example so think your description is somewhat ambiguous or subject to misinterpretation on closer inspection.

vzn
  • 11,162
  • 1
  • 28
  • 52