How can I build a regular expression that, using only the concatenate, union and star operations, over the alphabet {0,1}, describes the language "Every three consecutive characters contain at least two 1, and the input has length at least 3"? For instance 110011, 0101 and 11 should be refused. I was thinking on using the logic from this (incomplete) DFA, but I can't figure out how to get a regular expression that follows the rule. Thanks! 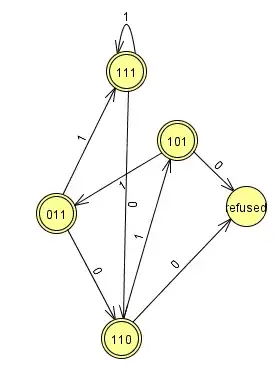
Asked
Active
Viewed 1,733 times
3
user1354784
- 309
- 3
- 14
1 Answers
1
Assume that string $s$ is in $L$. We will look at the last two characters of the string:
00, impossible, because this string could not be in $L$.01, next character must be 1, new last two characters is11.10, next character must be 1, new last two characters is01.11, next character may be 1 or 0, new last two characters is10or11.
Note that no matter your current state, you will always pass through the 11 state within two steps. Assuming that $s$ ended with 11, we get the following loop:
(1|(011))*
This will be the middle section of any string in $L$. All we need to do now is handle possible prefixes, making sure not to allow any with size < 3:
(111|011|1011|11011)
And finally, possible suffixes (note the empty union to express that the suffix is optional):
(|0|01)
Now all that's left is to concatenate them:
(111|011|1011|11011)(1|(011))*(|0|01)
orlp
- 13,988
- 1
- 26
- 41