6

I'm having some difficulty understanding the rules for valid red-black tree. If my understanding is correct there are 4 rules that a tree has to follow to be a red-black tree.

  1. Every node has a color either red or black.
  2. Root of tree is always black.
  3. There are no two adjacent red nodes (A red node cannot have a red parent or red child).
  4. Every path from root to a NULL node has same number of black nodes.

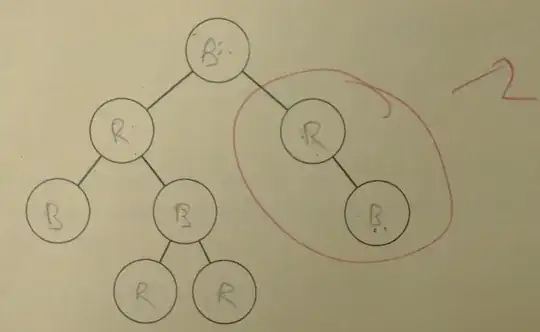
So I drew the tree below in a quiz, and apparently it's not valid. Could someone tell me why this tree is invalid? Invalid RB Tree

Thank you!

Raphael
  • 73,212
  • 30
  • 182
  • 400
Confused_CS_Student
  • 63
  • 1
  • 3

2 Answers2

5

If you go to the empty leaf from the root in the pattern [Right, Left], you get to an empty leaf encountering 1 black node. If you go [Right, Right, Left] or [Right, Right, Right], you get to an empty leaf hitting 2 black nodes. This is not allowed in a Red Black Tree because by definition a path from root to an empty leaf should contain the same amount of black nodes as every other path from root to an empty leaf.

The other important thing to know is that NULL nodes (leaves) aren't drawn; only the internal nodes are drawn. By convention, all leaves (NULL nodes) automatically are considered to be colored black.

D.W.
  • 167,959
  • 22
  • 232
  • 500
Cricket
  • 66
  • 2
0

There are 5 nodes with <2 children. In red-black trees, all nodes with <2 children must have the same black-depth, i.e. the number of black parents between it and the root, a black node with <2 children is a +1 in its own black depth. The node directly to the right of the root has black depth of 1 while every other node with <2 children has a black depth of 2.

LaTeX
  • 1
  • 1