6

Given a DAG (directed acyclic graph) $G=(V,E)$ without multiple edges, i.e., edges with the same source and target vertices, we define:

A vertex $v_j \in V$ is a diamond-join ($\Diamond_J$) vertex if there exists some other vertex $v_f \in V$ such that there are at least two vertex-disjoint paths (except $v_f$ and $v_j$) from $v_f$ to $v_j$.

Furthermore, we call such a corresponding vertex $v_f$ above a diamond-fork ($\Diamond_F$) vertex. And, we call such a pair $(v_f, v_j)$ above a diamond ($\Diamond$) pair.

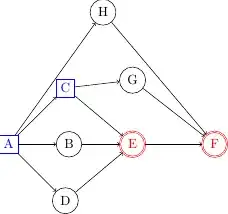
An Example: In the figure below,

  • $E$ and $F$ are $\Diamond_J$ vertices.
  • $A$ and $C$ are $\Diamond_F$ vertices.
  • $(A,E), (A,F)$ and $(C,F)$ are $\Diamond$ pairs.

diamond-dag

The problems are:

  1. How to identify all the $\Diamond_J$ vertices?
  2. How to identify all the $\Diamond_F$ vertices?
  3. How to identify all the $\Diamond$ pairs?

The algorithms should be as efficient as possible. For example, are there linear algorithms, i.e., in $\Theta(n + m)$, for them, where $|V| = n, |E| = m$?

My Thoughts:

The first problem is easy: Run DFS on $G$ and the vertices pointed to by cross edges are the $\Diamond_J$ vertices.

I do not know how to solve 2&3 efficiently.

Edit (2016-05-11): I accept the answer by @Chao Xu which solves the third problem in $O(nm)$ (I think it is correct; please peer review it). I am still open to possibly more efficient algorithm for the third problem, like $O(n+m)$.

hengxin
  • 9,671
  • 3
  • 37
  • 75

1 Answers1

3

$G=(V,E)$ is the graph we work on.

Problem 2: $\Diamond_F(reverse(G))=\Diamond_J(G)$, where $reverse(G)$ reverses all the edges of G.

Problem 3: This can be solved in $O(nm)$ time. For each vertex $s$, find all the pairs $(s,v)\in \Diamond$ in $O(m)$ time. To do this and split every outgoing edge $(s,v)$ with a new vertex $v'$. Namely, delete edge $(s,v)$, and replace it with $(s,v')$ and $(v',v)$. Find the dominator tree with source $s$ in the new graph, which can be done in linear time for dags.

$(s,v)\in \Diamond$ iff $v$ is the children of $s$ in the dominator tree and $v\in V$.

Chao Xu
  • 3,103
  • 19
  • 34