An Euclidean graph, by definition is
A weighted graph in which the weights are equal to the Euclidean lengths of the edges in a specified embedding
and a graph is called planar if
it can be drawn in a plane without graph edges crossing
lastly, a planar straight-line graph (PSLG) is
embedding of a planar graph in the plane such that its edges are mapped into straight line segments.
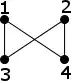
By these three definitions, I cannot conclude that if an Euclidean planar graph should be a PSLG or not. For instance, given an Euclidean non-planar graph:
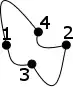
I can convert this graph into an Euclidean planar graph
by sticking with the definitions. Given the definitions above, the former one is a non planar straght-line graph whereas the latter one is a planar graph. Assume that the length of each edge is preserved. Then is the latter one still an Euclidean graph?