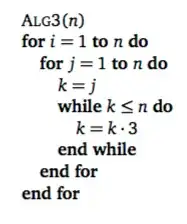Runtime for algorithm

Question

I need to get the asymptotic runtime for an algorithm and I'm just stuck.

A python implementation:

def alg3(n):
    for i in range(1, n+1):
        for j in range(1, n+1):
            k = j
            while k <= n:
                k = k*3

I think it should somehow be $\Theta(n^2\log(n))$ but that isn't quadratic. Can you help?

import time

def alg3(n):
    count = 0
    for i in range(1, n+1):
        for j in range(1, n+1):
            k = j
            while k <= n:
                count = count + 1
                k = k*3
    print(count)

n = 10
for i in range(0, 6):
    start_time = time.time()
    # run two times then calculate average time
    for i in range(0, 100):
        alg3(n)
    print("time with size %s: %s seconds" % (n, (time.time() - start_time)/100))
    n = n*2

If you calculate the factors given they give about 4.1.

score 4 · Answer 1 · answered Feb 28 '16 at 15:26

Let $f(n) = n^2\log n$, with the $\log$ taken to base 2. Then $$ \frac{f(2n)}{f(n)} = 4 \frac{\log(2n)}{\log n} = 4 \left(1 + \frac{1}{\log n}\right). $$ That is, for large $n$ you would expect $f(2n) \approx 4f(n)$. This shows that this test isn't sensitive enough to detect logarithmic factors.

score 3 · Answer 2 · answered Feb 28 '16 at 21:19

Let $f$ be the runtime of your algorithm, it's easy to find a close form $$ f(n) = n \sum_{j=1}^n \log_3 \left\lceil \frac{n}{j}\right\rceil $$

Then some calculations, $$ \begin{aligned} f(n) &\leq n + \frac1{\ln 3} n \sum_{j=1}^n \ln (\frac{n}{j}) \\ &\leq n + \frac1{\ln 3} n \int_{0}^{n} \ln (\frac{n}{x}) \mathrm{d}x \\ &= n + \frac1{\ln 3} n^2 \end{aligned} $$

Similarly, you can lower bound $f$.

$f(n) = \frac1{\ln 3} n^2 + O(n)$.

Runtime for algorithm

2 Answers2